- It's quite hard to distinguish between $D_8$ and $Q_8$ as groups, e.g. when trying to find the Galois group of a polynomial. Note that $Q_8$ only has one element of order 2, and it commutes with everything. If your group is going to be $D_8$, there's a good chance that complex conjugation won't commute with stuff, if it's your 2-cycle.
- If you're trying to analyse algebraic relations in the Galois group, you can use transitivity to produce explicit examples of automorphisms (in general it's quite hard to state an automorphism other than obvious conjugation explicitly). Just knowing that $\sigma$ sends $x_1$ to $x_2$ might be enough to help you out (e.g. when you need something that doesn't commute with complex conjugation).
- Critically, remember the (basic) fact that if you've proven your polynomial is irreducible, then it is the minimal polynomial for each of its roots. (Don't make the mistake of assuming this in general!) In particular, we know (for free) the dimension of the extension obtained by adjoining any one of the roots.
setsallthewaydown
Thursday, 8 May 2014
A couple of remarks in Galois Theory
Very short post today. Here are a couple of potentially useful Galois Theory-related things that I've discovered doing the 2005 past papers.
Monday, 24 March 2014
Probability and Measure - A properly Riemann Integrable function is Lebesgue integrable, and the values of the integrals coincide.
This post was inspired by an old argument that I had with Max about one of the P&M example sheets - were the integration signs supposed to represent Lebesgue integration or Riemann integration?
In previous years, Lebesgue integration was alluded to as an extension to Riemann integration, so we of course both suspected that they reduce to the same thing. Still, making the distinction does in fact matter - if we consider the expressions as Riemann integrals, it would not be valid to evaluate them using arguments based on monotone or dominated convergence.
I remember wondering why our lecturer never bothered to formally establish that Riemann integration is indeed a special case of Lebesgue integration. In this post, I hope to do exactly that. It's not quite as easy as you might have expected - there is a crucial subtlety involving null sets.
Recall the definition of Riemann integration, from Analysis I:
Interestingly, when researching this topic on the internet, I discovered that this definition of integration is actually usually called Darboux integration. What is usually called Riemann integration does not obtain upper and lower sums separately, but instead uses what wiki calls a tagged partition - given a partition, you also pick an arbitrary point $t_i$ inside each interval $[a_i,b_i]$ at which to evaluate the function, and then define the integral to be $\sum f(t_i)(b_i - a_i)$.
This is exactly how Dr. Dorrzapf defined Riemann integral when formally justifying more general constructions such as the path-integral in examples classes (although I vaguely remember that he arbitrarily set the tag $t_i$ to $a_i$).
The reason that our analysis lecturer could take such liberties with his impressionable Analysis students is that Darboux integration and Riemann integration are known to be equivalent. And, with the extra perspective gleaned from a beginner's course in measure theory, I think that his decision was fully justified - the upper and lower sum approach is much better preparation for the subsequent construction of Lebesgue integration.
Recall the definition of Lebesgue integration given in P&M. Our measure space is $([0,1], \mu)$, where $\mu$ is Lebesgue measure.
One slight quirk of notation - if $f$ is non-negative and measurable, $\mu(f)$ is defined whether or not $f$ is integrable.
The fundamental property of integration is the following:
The above property holds by construction for both Lebesgue and Riemann integrals.
Throughout the rest of this post, I will use the integral sign $\int$ to denote Riemann integration exclusively.
This is not quite sufficient to solve the problem as stated. To prove the full statement, we need to know that a Riemann integrable function is Lebesgue measurable. The proof of this result is actually more obscure than I thought it would be, drawing heavily from the properties of Lebesgue measure.
Recall the proof of Carathéodory's extension theorem, in which we construct the set $\mathcal{M}$ of outer-measurable sets. In fact, $M$ is the completion of the original $\sigma$-algebra, where by completion we mean that every subset of a set of zero measure is also measurable. Lebesgue measure is defined as the completion of the Borel measure on $\mathbb{R}$. This completeness property is precisely what we require.
In a non-complete measure space, the above lemma does not hold. If there exists a non-measurable set $Y$ that is a subset of a null set, then for any measurable function $f$, $g \equiv f + \chi_Y$ is equal to $f$ almost everywhere, but is not measurable.
In order to finish off, I'm going to use heavy machinery that I'm not going to prove (it's sufficiently interesting that I plan to revisit it in future, however).
Remark: from the discussion above, it is clear that there can exist a function that is Riemann integrable but not Borel measurable.
There are a few more things to say about the link between Riemann integration and Lebesgue integration. Tomorrow, I will post a short entry discussing examples of non-Riemann integrable functions that are Lebesgue integrable, as well as making a few remarks about improper Riemann integrals.
In previous years, Lebesgue integration was alluded to as an extension to Riemann integration, so we of course both suspected that they reduce to the same thing. Still, making the distinction does in fact matter - if we consider the expressions as Riemann integrals, it would not be valid to evaluate them using arguments based on monotone or dominated convergence.
I remember wondering why our lecturer never bothered to formally establish that Riemann integration is indeed a special case of Lebesgue integration. In this post, I hope to do exactly that. It's not quite as easy as you might have expected - there is a crucial subtlety involving null sets.
Recall the definition of Riemann integration, from Analysis I:
Let $f$ be a function of a closed interval, say $[0,1]$.
A partition $T$ of $[0,1]$ is an increasing sequence $0=t_0,t_1,\ldots,t_n=1$, which splits $[0,1]$ into $n$ intervals given by $[t_0,t_1]$, $[t_1,t_2]$, $\ldots$, $[t_{n-1}, t_n]$.
Define the lower sum over the partition $T$ to be $\displaystyle \sum_{i=0}^{n-1} \inf_{[t_i,t_{i+1}]} f$.
Define the upper sum over $T$ to be $\displaystyle \sum_{i=0}^{n-1} \sup_{[t_i,t_{i+1}]} f$.
$f$ is said to be integrable if, taking the supremum over the lower sums, and the infimum over the upper sums, the results both exist and coincide.
A partition $T$ of $[0,1]$ is an increasing sequence $0=t_0,t_1,\ldots,t_n=1$, which splits $[0,1]$ into $n$ intervals given by $[t_0,t_1]$, $[t_1,t_2]$, $\ldots$, $[t_{n-1}, t_n]$.
Define the lower sum over the partition $T$ to be $\displaystyle \sum_{i=0}^{n-1} \inf_{[t_i,t_{i+1}]} f$.
Define the upper sum over $T$ to be $\displaystyle \sum_{i=0}^{n-1} \sup_{[t_i,t_{i+1}]} f$.
$f$ is said to be integrable if, taking the supremum over the lower sums, and the infimum over the upper sums, the results both exist and coincide.
Interestingly, when researching this topic on the internet, I discovered that this definition of integration is actually usually called Darboux integration. What is usually called Riemann integration does not obtain upper and lower sums separately, but instead uses what wiki calls a tagged partition - given a partition, you also pick an arbitrary point $t_i$ inside each interval $[a_i,b_i]$ at which to evaluate the function, and then define the integral to be $\sum f(t_i)(b_i - a_i)$.
This is exactly how Dr. Dorrzapf defined Riemann integral when formally justifying more general constructions such as the path-integral in examples classes (although I vaguely remember that he arbitrarily set the tag $t_i$ to $a_i$).
The reason that our analysis lecturer could take such liberties with his impressionable Analysis students is that Darboux integration and Riemann integration are known to be equivalent. And, with the extra perspective gleaned from a beginner's course in measure theory, I think that his decision was fully justified - the upper and lower sum approach is much better preparation for the subsequent construction of Lebesgue integration.
Recall the definition of Lebesgue integration given in P&M. Our measure space is $([0,1], \mu)$, where $\mu$ is Lebesgue measure.
A simple function is a linear combination of indicator functions of measurable sets.
The integral $\mu(1_A)$ of the indicator function $1_A$ of a measurable set $A$ is defined to be $\mu(A)$. We extend this definition linearly to the set of simple functions.
Let $f$ be a non-negative, (Lebesgue) measurable function. The Lebesgue integral $\mu(f)$ is defined to be $\sup_G \mu(g)$, where $G$ is the set of simple functions dominated by $f$.
A general (measurable) function $f$ is said to be integrable if $\mu(|f|)$ is finite, in which case we define $\mu(f)=\mu(f^+)-\mu(f^-)$.
The integral $\mu(1_A)$ of the indicator function $1_A$ of a measurable set $A$ is defined to be $\mu(A)$. We extend this definition linearly to the set of simple functions.
Let $f$ be a non-negative, (Lebesgue) measurable function. The Lebesgue integral $\mu(f)$ is defined to be $\sup_G \mu(g)$, where $G$ is the set of simple functions dominated by $f$.
A general (measurable) function $f$ is said to be integrable if $\mu(|f|)$ is finite, in which case we define $\mu(f)=\mu(f^+)-\mu(f^-)$.
One slight quirk of notation - if $f$ is non-negative and measurable, $\mu(f)$ is defined whether or not $f$ is integrable.
The fundamental property of integration is the following:
If $f \leq g$ for any function $f$, $g$, then $\mu(f) \leq \mu(g)$.
The above property holds by construction for both Lebesgue and Riemann integrals.
Observation. A lower sum can be considered as a step function, i.e. a linear combination of indicator functions of (half-open) intervals.
Throughout the rest of this post, I will use the integral sign $\int$ to denote Riemann integration exclusively.
Corollary. If $f$ is Lebesgue measurable and Riemann integrable, then $f$ is Lebesgue integrable, and $\mu (f) = \int f \mathrm{d}x$.
Proof: $f$ is Riemann integrable, so there certainly exists one valid upper sum, meaning that $f$, and hence $|f|$, is bounded. Since we are in a finite measure space, $\mu(|f|) < \infty$, and so $f$ is Lebesgue integrable.
From the above observation, the set of lower sums can be considered as a subset of the set of simple functions. Let $G$ be the set of simple functions dominated by $f$, as before. Observe that every upper sum dominates $f$, and so every upper sum dominates every simple function in $G$. These two observations imply the following (you could worry about splitting $f$ up into positive and negative parts if you like, but there is zero difficulty involved):
$$\int f \mathrm{d}x = \sup\{\text{lower sums}\} \leq \sup_G \mu(g) = \mu(f) \leq \inf\{\text{upper sums}\} = \int f \mathrm{d}x $$
So $\int f \mathrm{d}x = \mu(f)$, as required. $\square$
From the above observation, the set of lower sums can be considered as a subset of the set of simple functions. Let $G$ be the set of simple functions dominated by $f$, as before. Observe that every upper sum dominates $f$, and so every upper sum dominates every simple function in $G$. These two observations imply the following (you could worry about splitting $f$ up into positive and negative parts if you like, but there is zero difficulty involved):
$$\int f \mathrm{d}x = \sup\{\text{lower sums}\} \leq \sup_G \mu(g) = \mu(f) \leq \inf\{\text{upper sums}\} = \int f \mathrm{d}x $$
So $\int f \mathrm{d}x = \mu(f)$, as required. $\square$
This is not quite sufficient to solve the problem as stated. To prove the full statement, we need to know that a Riemann integrable function is Lebesgue measurable. The proof of this result is actually more obscure than I thought it would be, drawing heavily from the properties of Lebesgue measure.
Recall the proof of Carathéodory's extension theorem, in which we construct the set $\mathcal{M}$ of outer-measurable sets. In fact, $M$ is the completion of the original $\sigma$-algebra, where by completion we mean that every subset of a set of zero measure is also measurable. Lebesgue measure is defined as the completion of the Borel measure on $\mathbb{R}$. This completeness property is precisely what we require.
Lemma. In a complete measure space, if $f$ is measurable, and $f=g$ almost everywhere, then $g$ is also measurable.
Proof: Write $\{f=g\}$ and $\{f \neq g\}$ for the sets on which $f=g$ and $f \neq g$ respectively. These are both measurable, and $\{f \neq g \}$ has measure zero, so every subset of it is measurable.
Given a measurable set $A \subseteq \mathbb{R}$, $g^{-1}(A)=(\left.g\right|_{f \neq g})^{-1}(A)\cup(\left.g\right|_{f = g})^{-1}(A)=(\left.g\right|_{f \neq g})^{-1}(A)\cup(\left.f\right|_{f = g})^{-1}(A)$. But $(\left.g\right|_{f \neq g})^{-1}(A)$ is a subset of the null set $\{f \neq g\}$, so is measurable, and $(\left.f\right|_{f = g})^{-1}(A)$ is also measurable.
Hence $g$ is measurable. $\square$
Given a measurable set $A \subseteq \mathbb{R}$, $g^{-1}(A)=(\left.g\right|_{f \neq g})^{-1}(A)\cup(\left.g\right|_{f = g})^{-1}(A)=(\left.g\right|_{f \neq g})^{-1}(A)\cup(\left.f\right|_{f = g})^{-1}(A)$. But $(\left.g\right|_{f \neq g})^{-1}(A)$ is a subset of the null set $\{f \neq g\}$, so is measurable, and $(\left.f\right|_{f = g})^{-1}(A)$ is also measurable.
Hence $g$ is measurable. $\square$
In a non-complete measure space, the above lemma does not hold. If there exists a non-measurable set $Y$ that is a subset of a null set, then for any measurable function $f$, $g \equiv f + \chi_Y$ is equal to $f$ almost everywhere, but is not measurable.
In order to finish off, I'm going to use heavy machinery that I'm not going to prove (it's sufficiently interesting that I plan to revisit it in future, however).
Theorem. (Riemann-Lebesgue) A function $f$ is Riemann integrable $\Leftrightarrow$ $f$ is bounded and continuous almost everywhere.
Corollary. If $f$ is Riemann integrable, then $f$ is (Lebesgue) measurable.
Proof: By the theorem, $f$ is equal almost everywhere to the function $g$ which is continuous on a measurable set, and zero on its complement. $g$ is clearly measurable, so using completeness of Lebesgue measure, $f$ is also measurable. $\square$
Conclusion. If $f$ is properly Riemann integrable, then $f$ is Lebesgue integrable, and the Riemann and Lebesgue integrals coincide.
Remark: from the discussion above, it is clear that there can exist a function that is Riemann integrable but not Borel measurable.
There are a few more things to say about the link between Riemann integration and Lebesgue integration. Tomorrow, I will post a short entry discussing examples of non-Riemann integrable functions that are Lebesgue integrable, as well as making a few remarks about improper Riemann integrals.
Labels:
integration,
lebesgue,
probability and measure,
riemann
Sunday, 23 March 2014
Graph Theory - The Four-Colour Theorem
The Four-Colour Theorem states that the faces of every planar graph can be coloured with four colours, without ever colouring two contiguous faces the same. A first (supposed) proof of the theorem was given in 1976, relying heavily on the output of a specially designed computer program.
This computer-assisted proof of the Four-Colour Theorem was catalytic (maybe even cataclysmic) in the maths world, challenging the sanctity of home-baked proofs traditionally written in sweat and blood. Historically, the meta-mathematical discussion resulting from this event has often been misrepresented - mathematicians did not object to the computer-assisted approach out of elitism or Luddism, but were genuinely uneasy about how they could be sure that the proposed solution actually constituted an acceptable proof. As it turns out, these misgivings were entirely justified - a team of researchers attempting to verify the original proof of the four-colour theorem were unable to decipher and reproduce the method from the 1976 paper, and were forced to come up with their own solution.
The proof of the FCT has been simplified and improved over the years, but still requires significant computer assistance, so it's understandable that it didn't feature in our course. We did however prove the weaker 5-colour theorem, and derived a very attractive equivalent formulation of the FCT. We also introduced and discussed a couple of interesting objects that were designed in an attempt to prove the FCT. One example is the chromatic polynomial $P_G(x)$, equal to the number of colourings of a graph $G$ in $x$ colours (it's a polynomial for combinatorial reasons). However, in an attempt to limit the scope of my post, I will leave the chromatic polynomial for another day.
Observe that a $k$-colouring of a graph immediately gives a $k$-partition of the vertices of $G$ with no edges within each partition, so colourings are actually highly valuable in practice.
In general, we are interested in the problem of finding an upper bound for $\chi(G)$. The greedy algorithm gives a first stab at this, but usually performs pretty awfully.
Note that the chromatic number is related to vertex-colourings, whereas the FCT concerns face-colourings. The following construction relates the two problems for the class of planar graphs.
Thus, proving that $\chi(G) \leq 4$ for every planar graph is equivalent to the usual statement of the FCT, which asserts that every bridgeless plane map can be face-coloured with four colours. (Quick terminological clarification - map indicates that we are referring to the faces of the graph. A plane graph (or map) is a given instance/embedding/realisation of a planar graph (or map), which is an abstract object. A planar graph can have several different plane graphs whose faces have different numbers of edges, although Euler's formula guarantees that the number of faces must remain constant.)
The following, weaker statement can be proven relatively easily from basic principles.
Here is a visual example of the construction used in the above proof:
The Four-Colour Theorem improves upon the above result by showing that $\chi(G)\leq4$ for every planar graph $G$. It is a best possible result - the planar graph $K_4$ certainly requires four distinct colours. As remarked above, its proof is everything but elementary. However, there is an interesting reformulation of the problem that we will take a moment to consider.
At any vertex with degree more than three, we can consider instead the graph obtained by introducing a polygonal roundabout. A face-colouring of the latter induces a face-colouring of the former.
Alternatively, you can make the same observation by considering a triangulation of the dual graph.
In my humble opinion, that proof is pretty damn awesome. Don't you agree?
Credit for the wording of the proofs should go to Prof. Thomason.
This computer-assisted proof of the Four-Colour Theorem was catalytic (maybe even cataclysmic) in the maths world, challenging the sanctity of home-baked proofs traditionally written in sweat and blood. Historically, the meta-mathematical discussion resulting from this event has often been misrepresented - mathematicians did not object to the computer-assisted approach out of elitism or Luddism, but were genuinely uneasy about how they could be sure that the proposed solution actually constituted an acceptable proof. As it turns out, these misgivings were entirely justified - a team of researchers attempting to verify the original proof of the four-colour theorem were unable to decipher and reproduce the method from the 1976 paper, and were forced to come up with their own solution.
The proof of the FCT has been simplified and improved over the years, but still requires significant computer assistance, so it's understandable that it didn't feature in our course. We did however prove the weaker 5-colour theorem, and derived a very attractive equivalent formulation of the FCT. We also introduced and discussed a couple of interesting objects that were designed in an attempt to prove the FCT. One example is the chromatic polynomial $P_G(x)$, equal to the number of colourings of a graph $G$ in $x$ colours (it's a polynomial for combinatorial reasons). However, in an attempt to limit the scope of my post, I will leave the chromatic polynomial for another day.
The chromatic number of a graph $G$, written $\chi(G)$, is the minimum number of colours required to colour the vertices of $G$ such that no two adjacent vertices have the same colour.
Observe that a $k$-colouring of a graph immediately gives a $k$-partition of the vertices of $G$ with no edges within each partition, so colourings are actually highly valuable in practice.
In general, we are interested in the problem of finding an upper bound for $\chi(G)$. The greedy algorithm gives a first stab at this, but usually performs pretty awfully.
Note that the chromatic number is related to vertex-colourings, whereas the FCT concerns face-colourings. The following construction relates the two problems for the class of planar graphs.
The dual graph $G^\prime$ of $G$ is the graph obtained by placing a vertex inside each face of $G$, and linking two vertexes together (in $G^\prime$) whenever the corresponding faces are continguous (in $G$). Visually, we draw one dual edge through each existing edge.
Above is an example of a self-dual graph on 5 vertices. Note that in general, the dual graph of a planar graph may fail to be simple (i.e. there could be could be multiple edges between two vertices, if $G$ has two faces that share multiple edges, or if there is a bridge). One sufficient condition for the dual to be simple is for $G$ to be $3$-connected, which means that removing any two vertices (and their incident edges) would not suffice to disconnect the graph.
Clearly the dual is planar. You can also visually recognise quite easily that the double-dual is naturally isomorphic to the original graph.
Observation. A vertex-colouring of $G$ is equivalent to a face-colouring of the dual graph $G^\prime$.
Thus, proving that $\chi(G) \leq 4$ for every planar graph is equivalent to the usual statement of the FCT, which asserts that every bridgeless plane map can be face-coloured with four colours. (Quick terminological clarification - map indicates that we are referring to the faces of the graph. A plane graph (or map) is a given instance/embedding/realisation of a planar graph (or map), which is an abstract object. A planar graph can have several different plane graphs whose faces have different numbers of edges, although Euler's formula guarantees that the number of faces must remain constant.)
The following, weaker statement can be proven relatively easily from basic principles.
Theorem. (Five-Colour Theorem)
If $G$ is a planar graph, then $\chi(G)\leq 5$.
If $G$ is a planar graph, then $\chi(G)\leq 5$.
Proof: Suppose not. Let $G$ be a minimal counterexample.
Recall (from an earlier post) that for any planar graph, the minimum degree $\delta(G)$ satisfies $\delta(G) \leq 5$.
We first consider the case $\delta(G) \leq 4$. Let $v$ be a vertex of degree $\leq 4$. By minimality, we can colour $G-v$ with 5 colours. But $v$ has at most 4 neighbours in $G$, so we can certainly colour $v$ with one of the 5 colours, giving a 5-colouring of $G$.
So we may assume $\delta(G)=5$.
Pick a vertex of degree 5, with neighbours $v_1$, $v_2$, $v_3$, $v_4$, and $v_5$.
$K_5$ is non-planar, so is not a subgraph of $G$. Thus, we can pick $v_i$ and $v_j$ such that $v_iv_j$ is not an edge. We construct a new graph, $G^\prime$, by removing $v$, and identifying $v_i$ and $v_j$.
This graph is planar by construction, so can be 5-coloured by minimality.
But we can use this colouring to colour $G$. In $G$, colour both $v_i$ and $v_j$ the same colour as the identified vertex in $G^\prime$ (every other vertex apart from $v$ can keep its colour). But now the neighbours of $v$ use only 4 colours, so we can use the 5th colour to complete the 5-colouring of $G$. $\square$
Recall (from an earlier post) that for any planar graph, the minimum degree $\delta(G)$ satisfies $\delta(G) \leq 5$.
We first consider the case $\delta(G) \leq 4$. Let $v$ be a vertex of degree $\leq 4$. By minimality, we can colour $G-v$ with 5 colours. But $v$ has at most 4 neighbours in $G$, so we can certainly colour $v$ with one of the 5 colours, giving a 5-colouring of $G$.
So we may assume $\delta(G)=5$.
Pick a vertex of degree 5, with neighbours $v_1$, $v_2$, $v_3$, $v_4$, and $v_5$.
$K_5$ is non-planar, so is not a subgraph of $G$. Thus, we can pick $v_i$ and $v_j$ such that $v_iv_j$ is not an edge. We construct a new graph, $G^\prime$, by removing $v$, and identifying $v_i$ and $v_j$.
This graph is planar by construction, so can be 5-coloured by minimality.
But we can use this colouring to colour $G$. In $G$, colour both $v_i$ and $v_j$ the same colour as the identified vertex in $G^\prime$ (every other vertex apart from $v$ can keep its colour). But now the neighbours of $v$ use only 4 colours, so we can use the 5th colour to complete the 5-colouring of $G$. $\square$
Here is a visual example of the construction used in the above proof:
 |
 |
| $G$ | $G^\prime$ |
The Four-Colour Theorem improves upon the above result by showing that $\chi(G)\leq4$ for every planar graph $G$. It is a best possible result - the planar graph $K_4$ certainly requires four distinct colours. As remarked above, its proof is everything but elementary. However, there is an interesting reformulation of the problem that we will take a moment to consider.
We define $\chi^\prime(G)$, the edge-chromatic number, to be the minimum number of colours needed to colours the edges of $G$ such that no two adjacent edges are coloured the same.
A cubic graph is a 3-regular graph, meaning that every vertex has exactly three neighbours.
Observation. To prove the FLT (in it's face-colouring form), we may assume that $G$ is cubic.
At any vertex with degree more than three, we can consider instead the graph obtained by introducing a polygonal roundabout. A face-colouring of the latter induces a face-colouring of the former.
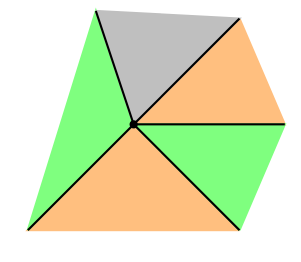 |

|
Theorem (Tait)
The FCT holds $\Leftrightarrow$ $\chi^\prime(G)=3$ for every cubic planar bridgeless graph $G$.
The FCT holds $\Leftrightarrow$ $\chi^\prime(G)=3$ for every cubic planar bridgeless graph $G$.
Proof: Let $G$ be a cubic bridgeless planar graph. We show that $G$ can be face 4-coloured $\Leftrightarrow$ $G$ can be edge 3-coloured.
Consider $\mathbb{Z}_2\times\mathbb{Z}_2$ as an additive group - containing four elements: 00, 01, 10, 11. These will be our four face-colours, and we will find a corresponding edge-colouring using only 01,10 and 11.
Given a face colouring, let each edge be coloured with the sum of the two bordering face colours. Since $G$ is bridgeless, no edge will be coloured 00. Also, no two adjacent edges will get the same colour, as $a+c \neq b+c$ if $a \neq b$ (recall that we are considering cubic graphs, so there are always exactly three edges incident to a given vertex).
Given an edge colouring, we need to find a face 4-colouring. We will do this by vertex-colouring the dual (observe that the dual of a cubic graph is a triangulation). Each edge of the dual crosses exactly one edge in the original graph. For each edge in the dual, record this initial colour (as a label).
Pick a vertex $v_0$ in the dual, and colour it 00. To obtain the final colour for any other vertex $v$, sum up the labels along any path between $v_0$ and $v$.
The sum of the labels around any triangle is 10+01+11=00, and so the sum of the labels around any cycle vanishes. This proves that the sum of the labels along a path between $v$ and $v_0$ is independent of the path, so the above colouring is well-defined. $\square$
Consider $\mathbb{Z}_2\times\mathbb{Z}_2$ as an additive group - containing four elements: 00, 01, 10, 11. These will be our four face-colours, and we will find a corresponding edge-colouring using only 01,10 and 11.
Given a face colouring, let each edge be coloured with the sum of the two bordering face colours. Since $G$ is bridgeless, no edge will be coloured 00. Also, no two adjacent edges will get the same colour, as $a+c \neq b+c$ if $a \neq b$ (recall that we are considering cubic graphs, so there are always exactly three edges incident to a given vertex).
Given an edge colouring, we need to find a face 4-colouring. We will do this by vertex-colouring the dual (observe that the dual of a cubic graph is a triangulation). Each edge of the dual crosses exactly one edge in the original graph. For each edge in the dual, record this initial colour (as a label).
Pick a vertex $v_0$ in the dual, and colour it 00. To obtain the final colour for any other vertex $v$, sum up the labels along any path between $v_0$ and $v$.
The sum of the labels around any triangle is 10+01+11=00, and so the sum of the labels around any cycle vanishes. This proves that the sum of the labels along a path between $v$ and $v_0$ is independent of the path, so the above colouring is well-defined. $\square$
In my humble opinion, that proof is pretty damn awesome. Don't you agree?
Credit for the wording of the proofs should go to Prof. Thomason.
Friday, 21 March 2014
Number Theory, Topics in Analysis: Continued fractions and Diophantine approximation
The Number Theory and Topics in Analysis courses complement each other surprisingly well on the topic of continued fractions. In Number Theory, they were introduced ultimately as a means to an end - a technique for solving Pell's equation, and a prime factorisation algorithm. The TinA approach was vastly more contemplative, presenting continued fractions as a (slightly feeble) attempt to understand some aspects of the nature of real numbers.
The rational numbers are dense in the real numbers. Yet there are lots more real numbers than rational numbers. In order to make any sense at all out of this, we need to be less careless. One possible approach is to quantify the cost or effectiveness of a given rational approximation, by measuring the size of the denominator you have to resort to in order to make it happen (compare this to the degree of the polynomials used to uniformly approximate continuous functions).
The results of this idea are ultimately quite surprising. We obtain a hierarchy of types of real number, based on how costly they are to approximate. The real numbers that are hardest to approximate are what we intuitively consider to be the most regular class of reals - the rational numbers themselves. What?
Thus, real numbers with repeating decimal expansions correspond to a particular subclass of numbers - the rationals. We will later remark that real numbers with repeating continued fractions also correspond to a interesting subclass - quadratic algebraic numbers.
In this section, we consider the problem of finding a rational number close to an arbitrary real number $\alpha$.
As explained in the introduction, we are mainly interested in obtaining lower bounds for the cost. But no lower bound is complete without an upper bound. The following theorem is the much-needed reality check that I'm very surprised didn't come up in TinA - for any real number, the cost is never going to get pathologically bad.
Still, let's not get too optimistic about this. With the obvious caveat that any fraction "approximates" its own equivalence class perfectly, rational numbers are awful at approximating other rationals.
Algebraic numbers are slightly better, but still fairly poor.
Consider now a new class of real numbers, the diophantine numbers, which we didn't discuss directly in lectures. In order to motivate the definition, recall Roth's theorem, which was stated (incorrectly!) in lectures as an improvement on Liouville's theorem.
(In lectures, this was stated as $\forall \varepsilon$, $\exists c$ such that $\forall \alpha \ldots$, which is incorrect - the constant $c$ depends on $\alpha$.)
In other words, Theorem 1.4 says that every algebraic number is Diophantine. (Note: there may be other names for this class of numbers - they seem to be discussed very little on wiki. My source for this name is Terry Tao's blog. Not to be confused with Diophantine sets, which are discussed on wiki, and are related to recursively enumerable sets.)
These results already suffice to establish the table presented in the introduction. Interestingly, we have shown that the set of numbers that you can approximate very well with rationals is small in the sense of measure, but large in the sense of the Baire Category Theorem.
We have also set the stage for a technique for proving transcendentality - if you can prove that a given number violates the Liouville lower bound, or the stronger Roth lower bound, you can deduce that it's transcendental. An example of this is the Liouville number given in lectures, or more generally the uncountable set of Liouville numbers constructed in Example Sheet 4:
Open question (that I want to come back to, but haven't had time to think about yet) - are the above Liouville numbers Diophantine?
We will define continued fractions using the continued fraction algorithm, define the convergent sequences $p_n$ and $q_n$ independently, and then proceed to derive the link between the two. This presentation is backwards compared to the one given in TinA, but it avoids all of the tautologies that everyone was complaining about.
By construction, $[a_0;a_1] = a_0 + \frac{1}{a_1}$, $[a_0;a_1,a_2]= \displaystyle a_0 \frac{1}{a_1 + \frac{1}{a_2}}$, etc, so we recover the characteristic tower form of the continued fraction.
Note that $a_n \in \mathbb{N}$, except for $a_0$, which is in $\mathbb{Z}$.
Obviously, the first thing we want to show is that the convergents converge to $\alpha$ under the Euclidean metric. However, as things currently stand, the partial continued fractions are unwieldy objects. We introduce two intermediate sequences which are easier to manipulate, and which we will show contain all of the information given by the convergents.
[Note to self: investigate link with Euclidean division algorithm.]
Here are some elementary properties of this sequence, which we will use later on.
We now know enough to go ahead and prove that continued fractions converge to their value.
We have now laid the groundwork for our study of Diophantine approximation via continued fractions. We are not just interested in the fact that continued fractions converge to their value, but also in some intriguing features of their convergence. We will show that continued fractions provide the most cost-effective way to converge to any real, and, remarkably, that the continued fraction algorithm necessarily produces every good approximation - in other words, if a given approximation is particularly cheap, it will naturally arise as one of the convergents defined above.
Firstly, we show that, considered absolutely, the convergence is monotone - every convergent gives a better approximation than the last.
However, the partial continued fractions oscillate around their limit $\theta$, via the following observation.
As promised, we now prove that the convergents are the best approximants for a fixed cost.
And finally, if any approximation is particularly cost-efficient, it must in fact be a convergent.
The whole point of this section was to show that continued fractions do indeed provide insight about Diophantine approximation. The above result achieves this pretty spectacularly.
This generalises. There is a full characterisation of numbers with repeating continued fractions (much like section 0 gives a full characterisation of numbers with repeating decimal expansion), given by the following theorem.
For square roots, we can say more. The following theorem gives an excellent error-detecting failsafe for those awkward times when you find yourself needing to calculate the continued fraction of a square root in real time at the supermarket check-out.
The proofs of these theorems were not given in my course. However, I have an idea which might suffice to prove a watered-down version of 3.2. Watch this space.
This checks out with the excruciatingly simple example given in TinA: $\sqrt{2} = [1;\overline{2}]$. For the eager beavers out there, you can check that this is coherent with your calculations for $\sqrt{3}$. (On a Number Theory example sheet, we had to calculate $\sqrt{46}$, which is 12-periodic, and thus somewhat sadistic. Side-note: to find a higher period you have to go up to $\sqrt{94}$. Coincidence? I think not.)
One excellent application for which continued fractions are crucial is Pell's equation.
Pell's equation is useful for example in Number Fields, where solutions correspond to units of a given real quadratic field extension (the norm of $x+y \sqrt N$ is defined to be $x^2-Ny^2$).
We can use continued fractions to prove that Pell's equation can always be solved. We won't go through the method fully here, as it largely irrelevant to the TinA course, but let us at least make the following observation.
By considering the period of the continued fraction of $\sqrt N$, you can pick out the convergents that give solutions. Dirichlet's Unit Theorem merits a quick shout-out at this point - by pushing this line of reasoning further, you can show that the solutions to Pell's equation (corresponding to non-trivial units in $\mathbb{Q}(\displaystyle \sqrt N)$) form a (cyclic!) group, which is mind-blowingly cool.
A second application of continued fractions also exploits the nice properties of square roots - prime factorisation. This application is sort of technical, so I won't go into it right now, although I am planning a future post dedicated to prime factorisation algorithms.
There is a generalisation of continued fractions called (rather obscurely) "generalised continued fractions". I unfortunately do not have much to say about these at this point in time, other than the $\tan x$ example given in lectures was one of them.
This post has turned out to be massively long, as it was far too ambitious in scope. There are still a few details that I want to investigate in full depth at some point, but it's probably a better idea to do so in another post. I hope that anybody reading enjoyed it, and maybe learned something new.
Footnote: a significant number of these proofs are largely due to my Number Theory lecturer, Dr. Vicky Neale. A couple of them are due to my Topics in Analysis lecturer, Dr. Kovalev.
The rational numbers are dense in the real numbers. Yet there are lots more real numbers than rational numbers. In order to make any sense at all out of this, we need to be less careless. One possible approach is to quantify the cost or effectiveness of a given rational approximation, by measuring the size of the denominator you have to resort to in order to make it happen (compare this to the degree of the polynomials used to uniformly approximate continuous functions).
The results of this idea are ultimately quite surprising. We obtain a hierarchy of types of real number, based on how costly they are to approximate. The real numbers that are hardest to approximate are what we intuitively consider to be the most regular class of reals - the rational numbers themselves. What?
| Class of real numbers | Measure (per unit) | Cardinality | Category | Cost of approximating | |
|---|---|---|---|---|---|
| Algebraic numbers | Rationals | 0 | $\aleph_0$ | Meagre | Disastrous |
| Irrational algebraics | 0 | $\aleph_0$ | Meagre | Meh | |
| Transcendental numbers | Diophantine transcendentals | 1 | $\mathfrak{c}$ | Meagre | |
| Non-Diophantine transcendentals | 0 | $\mathfrak{c}$ | Residual | Good |
The aim of this post is to establish the above results, as well as providing a more general panorama of continued fractions, their properties, and their applications. I will include results and concepts from both courses, so hopefully anybody reading this will enjoy and benefit from a slightly expanded perspective.
Section 0: A word on decimal expansions
We will show later that continued fractions correspond bijectively with real numbers. So, in some sense, they are an alternative way of representing reals, as opposed to the more familiar decimal expansion. The analogy pretty much stops there - as far as I can tell, there is little to gain in comparing the two systems. Still, I want to seize this opportunity to consider formally a couple of properties of decimals that are usually taken for granted, as we will briefly explore some analagous results for continued fractions.
Proposition 0.1 A real number with a repeating decimal expansion is a rational number.
Proof: Let $\alpha = d.d_1d_2d_3\dots d_m\overline{d_{m+1}\dots d_{m+k}}$. Then $10^m\alpha = N + 0.\overline{d_{m+1}\dots d_{m+k}}$, and $10^{m+k}\alpha=M + 0.\overline{d_{m+1}\dots d_{m+k}}$ for some integers $N$, $M$. Thus, $10^{m+k}\alpha - 10^m\alpha = K$ for some integer $K$, giving $\alpha = \frac{K}{10^{m+k}-10^k}$, and so $\alpha \in \mathbb{Q}$. $\square$ (proof found here).
Proposition 0.2 A rational number has a repeating decimal expansion.
Proof: Consider performing the calculation $\frac{p}{q}$ by long division. At each step, the remainder will be in $\{0,1,2,\ldots,q-1\}$. By the pigeonhole principle, a remainder must repeat after $q+1$ steps. But a repeated remainder forces the calculation into a loop. $\square$
Thus, real numbers with repeating decimal expansions correspond to a particular subclass of numbers - the rationals. We will later remark that real numbers with repeating continued fractions also correspond to a interesting subclass - quadratic algebraic numbers.
Section 1: Diophantine approximation
In this section, we consider the problem of finding a rational number close to an arbitrary real number $\alpha$.
As explained in the introduction, we are mainly interested in obtaining lower bounds for the cost. But no lower bound is complete without an upper bound. The following theorem is the much-needed reality check that I'm very surprised didn't come up in TinA - for any real number, the cost is never going to get pathologically bad.
Theorem 1.1 (Dirichlet's theorem) Let $\alpha$ be a real number. For every $N \in \mathbb{N}$ there exists a rational number $\frac{a}{q}$ with $1 \leq q < N$ and $\left| \alpha - \frac{a}{q}\right| \leq \frac{1}{qN}$.
Proof: Consider the fractional part of the $N+1$ distinct numbers $k\theta$, for $0 \leq k \leq N$. Split the unit interval into the $N$ disjoint intervals of length $\frac{1}{N}$ given by $[\frac{j}{N},\frac{j+1}{N}]$, for $0 \leq j < N$.
By the pigeonhole principle, there must be an inteval containing two of the $k\theta$, say $k_1\theta$ and $k_2\theta$, $k_2>k_1$. But then for $q=k_2-k_1$, $|q \theta - a | \leq \frac{1}{N}$ for some integer $a$. By construction, $1\leq q \leq N$. $\square$
By the pigeonhole principle, there must be an inteval containing two of the $k\theta$, say $k_1\theta$ and $k_2\theta$, $k_2>k_1$. But then for $q=k_2-k_1$, $|q \theta - a | \leq \frac{1}{N}$ for some integer $a$. By construction, $1\leq q \leq N$. $\square$
Still, let's not get too optimistic about this. With the obvious caveat that any fraction "approximates" its own equivalence class perfectly, rational numbers are awful at approximating other rationals.
Proposition 1.2 If $\alpha = \frac{a}{b} \neq \frac{p}{q}$, then $\left|\alpha - \frac{p}{q}\right| \geq \frac{1}{bq}$.
Proof: $\left|\frac{a}{b}-\frac{p}{q}\right| = \left|\frac{aq-bp}{bq}\right| \geq \frac{1}{bq}$ $\square$
Algebraic numbers are slightly better, but still fairly poor.
Theorem 1.3 (Liouville's theorem) Let $\alpha$ be algebraic. Then $\exists c>0$ (depending on $\alpha$) such that $\left|\alpha - \frac{p}{q}\right| \geq \frac{c}{q^n}$, for every rational $\frac{p}{q}$, where $n$ is the degree of the minimal polynomial over $\mathbb{Z}$.
Proof: In lectures we only assumed that $f$ is an arbitrary polynomial with $\alpha$ as a root. However, using the minimal polynomial gives a better lower bound. Pick $R$ sufficiently large that all of the (real) roots of $f$ are contained inside $[-R+1,R-1]$. $f^\prime$ is continuous on $[-R,R]$, and so bounded, by $M$, say. For every rational $\frac{p}{q} \in [-R,R]$, if $f(\frac{p}{q}) \neq 0$, then $\frac{1}{q^n} \leq \left|f(\frac{p}{q})\right|= \left|f(\frac{p}{q})-f(\alpha)\right| \leq M \left| \frac{p}{q} -\alpha\right|$, by the mean value theorem.
There are only many finitely roots, so $\exists c_0$ such that $|\frac{p}{q}-\alpha| \geq c_0 \geq \frac{c_0}{q^n}$ for all rational roots $\frac{p}{q}$ of $f$ (which we secretly know have to be integers anyway).
Finally, if $\left|\frac{p}{q}\right| \geq R$, then $\left|\frac{p}{q} - \alpha \right| \geq 1 \geq \frac{1}{q^n}$.
So, by taking $c = \min\{\frac{1}{M},1,c_0\}$, we have found the required constant. $\square$
There are only many finitely roots, so $\exists c_0$ such that $|\frac{p}{q}-\alpha| \geq c_0 \geq \frac{c_0}{q^n}$ for all rational roots $\frac{p}{q}$ of $f$ (which we secretly know have to be integers anyway).
Finally, if $\left|\frac{p}{q}\right| \geq R$, then $\left|\frac{p}{q} - \alpha \right| \geq 1 \geq \frac{1}{q^n}$.
So, by taking $c = \min\{\frac{1}{M},1,c_0\}$, we have found the required constant. $\square$
Consider now a new class of real numbers, the diophantine numbers, which we didn't discuss directly in lectures. In order to motivate the definition, recall Roth's theorem, which was stated (incorrectly!) in lectures as an improvement on Liouville's theorem.
Theorem 1.4 (Thue-Siegel-Roth theorem) Let $\alpha$ be algebraic and irrational. Then for all $\varepsilon > 0$, $\exists c > 0$ such that $\left| \alpha - \frac{p}{q}\right| \geq \frac{c}{q^{2+\varepsilon}}$ for any rational number $\frac{p}{q}$.
(In lectures, this was stated as $\forall \varepsilon$, $\exists c$ such that $\forall \alpha \ldots$, which is incorrect - the constant $c$ depends on $\alpha$.)
Definition. Say that $\alpha \in \mathbb{R}$ is Diophantine if $\forall \varepsilon > 0$, $\exists c >0$ such that $\left| \alpha - \frac{p}{q}\right| \geq \frac{c}{q^{2+\varepsilon}}$ for any rational number $\frac{p}{q}$.
In other words, Theorem 1.4 says that every algebraic number is Diophantine. (Note: there may be other names for this class of numbers - they seem to be discussed very little on wiki. My source for this name is Terry Tao's blog. Not to be confused with Diophantine sets, which are discussed on wiki, and are related to recursively enumerable sets.)
Theorem 1.5 The set of Diophantine numbers has full measure, but is meagre.
Proof: This is actually an excellent exercice in both measure theory and linear analysis, so I won't reproduce the proof here, only link to a good exposition of it. $\square$
These results already suffice to establish the table presented in the introduction. Interestingly, we have shown that the set of numbers that you can approximate very well with rationals is small in the sense of measure, but large in the sense of the Baire Category Theorem.
We have also set the stage for a technique for proving transcendentality - if you can prove that a given number violates the Liouville lower bound, or the stronger Roth lower bound, you can deduce that it's transcendental. An example of this is the Liouville number given in lectures, or more generally the uncountable set of Liouville numbers constructed in Example Sheet 4:
Proposition 1.6 For any sequence $a_n$ taking values in $\{1,2\}$, $\sigma = \sum \frac{a_n}{10^{n!}}$ is transcendental.
Open question (that I want to come back to, but haven't had time to think about yet) - are the above Liouville numbers Diophantine?
Section 2: Continued fractions
We will define continued fractions using the continued fraction algorithm, define the convergent sequences $p_n$ and $q_n$ independently, and then proceed to derive the link between the two. This presentation is backwards compared to the one given in TinA, but it avoids all of the tautologies that everyone was complaining about.
Given a real number $\theta$, we obtain a sequence $a_0,a_1,\ldots$ recursively by applying the following algorithm.
Set $a_0=\lfloor \theta \rfloor$.
Define $\alpha_1 = \frac{1}{\theta - a_0}$ (so $\theta = a_0 + \frac{1}{\alpha_1}$).
Define $a_n=\lfloor \alpha_n \rfloor$, and set $\alpha_{n+1}=\frac{1}{\alpha_n - a_n}$.
If we ever encounter $a_n=\alpha_n$, we terminate the process.
We write $[a_0;a_1,a_2,\ldots]$ for the continued fraction with value $\alpha$. The partial continued fractions $[a_0]$, $[a_0;a_1]$, $[a_0;a_1,a_2]$, $\ldots$ are called the convergents of $\alpha$.
Set $a_0=\lfloor \theta \rfloor$.
Define $\alpha_1 = \frac{1}{\theta - a_0}$ (so $\theta = a_0 + \frac{1}{\alpha_1}$).
Define $a_n=\lfloor \alpha_n \rfloor$, and set $\alpha_{n+1}=\frac{1}{\alpha_n - a_n}$.
If we ever encounter $a_n=\alpha_n$, we terminate the process.
We write $[a_0;a_1,a_2,\ldots]$ for the continued fraction with value $\alpha$. The partial continued fractions $[a_0]$, $[a_0;a_1]$, $[a_0;a_1,a_2]$, $\ldots$ are called the convergents of $\alpha$.
By construction, $[a_0;a_1] = a_0 + \frac{1}{a_1}$, $[a_0;a_1,a_2]= \displaystyle a_0 \frac{1}{a_1 + \frac{1}{a_2}}$, etc, so we recover the characteristic tower form of the continued fraction.
Note that $a_n \in \mathbb{N}$, except for $a_0$, which is in $\mathbb{Z}$.
Proposition 2.1 The continued fraction algorithm terminates $\Leftrightarrow$ $\theta$ is rational.
Proof: If the algorithm terminates, then $\theta=[a_0;a_1,\ldots,a_n]$ for some $a_n$. By multiplying out the denominators in the tower form, it is obvious that $\theta$ is rational.
If $\theta$ is rational, then the $\alpha_i$ constructed in the algorithm are also rational. But by construction, their denominators are strictly decreasing, so the process must terminate. $\square$
If $\theta$ is rational, then the $\alpha_i$ constructed in the algorithm are also rational. But by construction, their denominators are strictly decreasing, so the process must terminate. $\square$
Obviously, the first thing we want to show is that the convergents converge to $\alpha$ under the Euclidean metric. However, as things currently stand, the partial continued fractions are unwieldy objects. We introduce two intermediate sequences which are easier to manipulate, and which we will show contain all of the information given by the convergents.
Define the sequences:
| $p_0 = a_0$ | $p_1=a_0a_1+1$ | $p_n=a_np_{n-1}+p_{n-2}$ |
| $q_0 = 1$ | $q_1=a_1$ | $q_n=a_nq_{n-1}+q_{n-2}$ |
[Note to self: investigate link with Euclidean division algorithm.]
Here are some elementary properties of this sequence, which we will use later on.
Proposition 2.2
- For each $n \geq 1$, $p_nq_{n-1}-p_{n-1}q_n=(-1)^{n+1}$.
- $p_n$ and $q_n$ are coprime.
Proof: For the first statement, we induct on $n$.
When $n=1$, $p_1q_0-p_0q_1=a_0a_1+1-a_0a_1=1$.
Suppose the relation holds for $n$, where $n \geq 1$.
Then $p_{n+1}q_n-p_nq_{n+1}=(a_{n+1}p_n+p_{n-1}q_n)q_n - p_n(a_{n+1}q_n+q_{n-1}) = p_{n-1}q_n-p_nq_{n-1}=(-1)^{n+2}$.
The second statement follows directly from the first (think of Bezout). $\square$
When $n=1$, $p_1q_0-p_0q_1=a_0a_1+1-a_0a_1=1$.
Suppose the relation holds for $n$, where $n \geq 1$.
Then $p_{n+1}q_n-p_nq_{n+1}=(a_{n+1}p_n+p_{n-1}q_n)q_n - p_n(a_{n+1}q_n+q_{n-1}) = p_{n-1}q_n-p_nq_{n-1}=(-1)^{n+2}$.
The second statement follows directly from the first (think of Bezout). $\square$
Proposition 2.3 $\frac{p_n}{q_n}=[a_0;a_1,\ldots,a_n]$ in its lowest form.
Proof: Let us relax our notation slightly to allow $\alpha_n$, the last term of $[a_0;a_1,\ldots,\alpha_n]$, to be an arbitrary (positive) real number. Under this notation, we can write $[a_0;a_1,\ldots,a_n,\alpha_{n+1}]=[a_0;a_1,\ldots,a_n+\frac{1}{\alpha_{n+1}}]$. This will hopefully make the calculations slightly clearer.
Observe that the claim is true for $n=0,1,2$ (this involves multiplying out the tower form of $[a_0;a_1,\alpha_2]$, and is absolutely trivial).
Assume that the claim is true for $n$.
$$\displaystyle \frac{p_{n+1}}{q_{n+1}} = \frac{\alpha_{n+1}p_n+p_{n-1}}{\alpha_{n+1}q_n+q_{n-1}} = \frac{p_n + \frac{1}{\alpha_{n+1}}p_{n-1}}{q_n+\frac{1}{\alpha_{n+1}}q_{n-1}}= \frac{(a_np_{n-1}+p_{n-2})+\frac{p_{n-1}}{\alpha_{n+1}}}{(a_nq_{n-1}+q_{n-2})+\frac{q_{n-1}}{\alpha_{n+1}}} = \frac{\left(a_n+\frac{1}{\alpha_{n+1}}\right)p_{n-1}+p_{n-2}}{\left(a_n+\frac{1}{\alpha_{n+1}}\right)q_{n-1}+q_{n-2}}=[a_0;a_1,\ldots,a_n+\frac{1}{\alpha_{n+1}}]=[a_0;a_1,\ldots,a_n,\alpha_{n+1}]$$
We used the induction hypothesis in the second-last equality.
We have already shown above that $p_n$, $q_n$ are coprime, so the fraction is necessarily in its lowest form. $\square$
Observe that the claim is true for $n=0,1,2$ (this involves multiplying out the tower form of $[a_0;a_1,\alpha_2]$, and is absolutely trivial).
Assume that the claim is true for $n$.
$$\displaystyle \frac{p_{n+1}}{q_{n+1}} = \frac{\alpha_{n+1}p_n+p_{n-1}}{\alpha_{n+1}q_n+q_{n-1}} = \frac{p_n + \frac{1}{\alpha_{n+1}}p_{n-1}}{q_n+\frac{1}{\alpha_{n+1}}q_{n-1}}= \frac{(a_np_{n-1}+p_{n-2})+\frac{p_{n-1}}{\alpha_{n+1}}}{(a_nq_{n-1}+q_{n-2})+\frac{q_{n-1}}{\alpha_{n+1}}} = \frac{\left(a_n+\frac{1}{\alpha_{n+1}}\right)p_{n-1}+p_{n-2}}{\left(a_n+\frac{1}{\alpha_{n+1}}\right)q_{n-1}+q_{n-2}}=[a_0;a_1,\ldots,a_n+\frac{1}{\alpha_{n+1}}]=[a_0;a_1,\ldots,a_n,\alpha_{n+1}]$$
We used the induction hypothesis in the second-last equality.
We have already shown above that $p_n$, $q_n$ are coprime, so the fraction is necessarily in its lowest form. $\square$
We now know enough to go ahead and prove that continued fractions converge to their value.
Proposition 2.4 If $[a_0;a_1,a_2,\ldots]$ is the continued fraction obtained from $\theta$ using the division algorithm, then $[a_0;a_1,\ldots,a_n] \to \theta$ as $n \to \infty$.
Proof: Using the relaxed notation from the above proposition, we can write $\theta = [a_0;a_1,\ldots,a_n,\alpha_{n+1}]$, which we know is equal to $\frac{\alpha_{n+1}p_n+p_{n-1}}{\alpha_{n+1}q_n+q_{n-1}}$. So:
$$\left| \theta - \frac{p_n}{q_n}\right| = \left|\frac{\alpha_{n+1}p_n+p_{n-1}}{\alpha_{n+1}q_n+q_{n-1}}-\frac{p_n}{q_n}\right| = \frac{|p_nq_{n-1}-p_{n-1}q_n|}{q_n(\alpha_{n+1}q_n+q_{n-1})}=\frac{1}{q_n(\alpha_{n+1}q_n+q_{n-1})}$$
But by considering the recurrence relation, we see that $q_n$ is a strictly increasing sequence of positive integers. The result follows. $\square$
$$\left| \theta - \frac{p_n}{q_n}\right| = \left|\frac{\alpha_{n+1}p_n+p_{n-1}}{\alpha_{n+1}q_n+q_{n-1}}-\frac{p_n}{q_n}\right| = \frac{|p_nq_{n-1}-p_{n-1}q_n|}{q_n(\alpha_{n+1}q_n+q_{n-1})}=\frac{1}{q_n(\alpha_{n+1}q_n+q_{n-1})}$$
But by considering the recurrence relation, we see that $q_n$ is a strictly increasing sequence of positive integers. The result follows. $\square$
We have now laid the groundwork for our study of Diophantine approximation via continued fractions. We are not just interested in the fact that continued fractions converge to their value, but also in some intriguing features of their convergence. We will show that continued fractions provide the most cost-effective way to converge to any real, and, remarkably, that the continued fraction algorithm necessarily produces every good approximation - in other words, if a given approximation is particularly cheap, it will naturally arise as one of the convergents defined above.
Firstly, we show that, considered absolutely, the convergence is monotone - every convergent gives a better approximation than the last.
Lemma 2.5 For each $n$, $\frac{1}{q_{n+2}} \leq | q_n \theta - p_n | \leq \frac{1}{q_{n+1}}$. This immediately implies that $|q_n\theta - p_n | \leq |q_{n-1} \theta - p_{n-1}|$, which further implies that $|\theta - \frac{p_n}{q_n}| \leq |\theta - \frac{p_{n-1}}{q_{n-1}}|$.
Proof: The key observation is that $a_{n+1} \leq \alpha_{n+1} \leq a_{n+1} + 1$. This gives $q_{n+1} = a_{n+1}q_n + q_{n-1} \leq \alpha_{n+1}q_n + q_{n-1} \leq (a_{n+1}+1)q_n+q_{n-1} = q_{n+1}+q_n \leq a_{n+2}q_{n+1}+q_n = q_{n+2}$.
Recalling that $|q_n \theta - p_n | = \frac{1}{\alpha_{n+1}q_n+q_{n-1}}$, from the proof of the previous proposition, we are done. $\square$
Recalling that $|q_n \theta - p_n | = \frac{1}{\alpha_{n+1}q_n+q_{n-1}}$, from the proof of the previous proposition, we are done. $\square$
However, the partial continued fractions oscillate around their limit $\theta$, via the following observation.
Lemma 2.6 For each $n$, $\theta - \frac{p_n}{q_n}$ and $\theta - \frac{p_{n-1}}{q_{n-1}}$ have opposite sign.
Proof: Go back to the proof of the above lemma, and observe that without the mod signs, we obtain $\theta - \frac{p_n}{q_n} = \frac{(-1)^n}{q_n(\alpha_{n+1}q_n+q_{n-1})}$. $\square$
As promised, we now prove that the convergents are the best approximants for a fixed cost.
Theorem 2.7 For any integers $p$ and $q$ such that $0 < q < q_n$, $|q\theta - p| \geq |q_n\theta - p_n|$.
Proof: Let $\begin{pmatrix} u \\ v \end{pmatrix} = \begin{pmatrix} q_{n-1} & p_{n-1} \\ q_n & p_n \end{pmatrix}\begin{pmatrix} p \\ q \end{pmatrix}$. Note that this matrix has determinant $\pm 1$, so is invertible (its inverse has integer coefficients). Therefore, we can write $p = up_{n-1}+vp_n$ and $q = uq_{n-1}+vq_n$ for some integers $u,v$.
So, $|q\theta - p| = |uq_{n-1} \theta + v q_n \theta - u p_{n-1} - vp_n | = |u (q_{n-1} \theta - p_{n-1}) + v(q_n \theta - p_n)|$.
However, we assumed that $0 < q < q_n$, so $0 < uq_{n-1} + vq_n < q_n$. This forces $u$ and $v$ to have opposite signs (if $v=0$ then $\frac{p}{q}=\frac{p_n}{q_n}$). Since $q_{n-1}\theta - p_{n-1}$ and $q_n\theta - p_n$ also have opposite signs by the above lemma, we can write:
$|q\theta - p| = |u(q_{n-1}\theta-p_{n-1})|+|v(q_n\theta - p_n)| \geq |q_{n-1}\theta - p_{n-1}|$. $\square$
So, $|q\theta - p| = |uq_{n-1} \theta + v q_n \theta - u p_{n-1} - vp_n | = |u (q_{n-1} \theta - p_{n-1}) + v(q_n \theta - p_n)|$.
However, we assumed that $0 < q < q_n$, so $0 < uq_{n-1} + vq_n < q_n$. This forces $u$ and $v$ to have opposite signs (if $v=0$ then $\frac{p}{q}=\frac{p_n}{q_n}$). Since $q_{n-1}\theta - p_{n-1}$ and $q_n\theta - p_n$ also have opposite signs by the above lemma, we can write:
$|q\theta - p| = |u(q_{n-1}\theta-p_{n-1})|+|v(q_n\theta - p_n)| \geq |q_{n-1}\theta - p_{n-1}|$. $\square$
And finally, if any approximation is particularly cost-efficient, it must in fact be a convergent.
Corollary 2.8 For any integer $p$ and positive integer $q$, if $|\theta - \frac{p}{q}| < \frac{1}{2q^2}$, then $\frac{p}{q}$ is one of the convergents of $\theta$.
Proof: Assume WLOG that $p$ and $q$ are coprime. Pick $n$ such that $q_n \leq q < q_{n+1}$ (recall the $q_n$ are a strictly increasing sequence of positive integers, and $q_0=1$, so we can do this).
Then $\left| \frac{p}{q} -\frac{p_n}{q_n}\right| \leq \left| \theta - \frac{p}{q}\right| + \left| \theta - \frac{p_n}{q_n}\right| < \frac{1}{2q^2} + \frac{1}{q_n}|q\theta - p| < \frac{1}{2qq_n}+\frac{1}{q_n}\frac{1}{2q} \leq \frac{1}{qq_n}$.
So, $\left|\frac{p}{q}-\frac{p_n}{q_n}\right| = \frac{|pq_n-p_nq|}{qq_n} < \frac{1}{qq_n}$, so $|pq_n-p_nq| < 1$.
We conclude that $pq_n-p_nq=0$, so $\frac{p}{q}=\frac{p_n}{q_n}$. $\square$
Then $\left| \frac{p}{q} -\frac{p_n}{q_n}\right| \leq \left| \theta - \frac{p}{q}\right| + \left| \theta - \frac{p_n}{q_n}\right| < \frac{1}{2q^2} + \frac{1}{q_n}|q\theta - p| < \frac{1}{2qq_n}+\frac{1}{q_n}\frac{1}{2q} \leq \frac{1}{qq_n}$.
So, $\left|\frac{p}{q}-\frac{p_n}{q_n}\right| = \frac{|pq_n-p_nq|}{qq_n} < \frac{1}{qq_n}$, so $|pq_n-p_nq| < 1$.
We conclude that $pq_n-p_nq=0$, so $\frac{p}{q}=\frac{p_n}{q_n}$. $\square$
The whole point of this section was to show that continued fractions do indeed provide insight about Diophantine approximation. The above result achieves this pretty spectacularly.
Section 3: Examples and applications
In general, computing the continued fraction of an arbitrary real is not very interesting - it is simply a matter of transforming the information we possess about that real (usually in the form of a decimal expansion) into the language of continued fractions.
If our chosen real number is rational, the algorithm terminates - which is hardly interestingly. Conversely, we have shown that if our real number is irrational it doesn't. We might therefore naively expect to have to do an infinite amount of work in order to achieve the full expansion. Tripos questions can be nasty, but hopefully not that nasty (even when PTJ is writing the questions).
However, in lectures, we saw the tantalising example of $\sqrt{2}$. Very quickly, the algorithm developped a loop, and so we could observe that the continued fraction expansion must necessarily repeat. On Example Sheet 4, we are asked to calculate the full expansion of $\sqrt{3}$, and so we might hope that something similiar is going to occur.
This generalises. There is a full characterisation of numbers with repeating continued fractions (much like section 0 gives a full characterisation of numbers with repeating decimal expansion), given by the following theorem.
A quadratic irrational is a root of a quadratic equation with integer coefficients. In the Number Fields course, we show that any such number must be of the form $a+b\sqrt{N}$ for some (square-free) integer $N$, and rationals $a$ and $b$.
Theorem 3.1 (Lagrange) For any real number $\theta$, $\theta$ is a quadratic irrational $\Leftrightarrow$ its continued fraction is (eventually) periodic.
For square roots, we can say more. The following theorem gives an excellent error-detecting failsafe for those awkward times when you find yourself needing to calculate the continued fraction of a square root in real time at the supermarket check-out.
Theorem 3.2 Let $N$ be a natural number that is not a square. Then its continued fraction is of the form $[a_0;\overline{a_1,a_2,\ldots,a_2,a_1,2a_0}]$. Thus, it is both periodic and symmetric, and each period ends on twice the integer part.
The proofs of these theorems were not given in my course. However, I have an idea which might suffice to prove a watered-down version of 3.2. Watch this space.
This checks out with the excruciatingly simple example given in TinA: $\sqrt{2} = [1;\overline{2}]$. For the eager beavers out there, you can check that this is coherent with your calculations for $\sqrt{3}$. (On a Number Theory example sheet, we had to calculate $\sqrt{46}$, which is 12-periodic, and thus somewhat sadistic. Side-note: to find a higher period you have to go up to $\sqrt{94}$. Coincidence? I think not.)
One excellent application for which continued fractions are crucial is Pell's equation.
Let $N$ be a natural number that is not a square. Pell's equation is given by:
$$x^2-Ny^2=1$$
$$x^2-Ny^2=1$$
Pell's equation is useful for example in Number Fields, where solutions correspond to units of a given real quadratic field extension (the norm of $x+y \sqrt N$ is defined to be $x^2-Ny^2$).
We can use continued fractions to prove that Pell's equation can always be solved. We won't go through the method fully here, as it largely irrelevant to the TinA course, but let us at least make the following observation.
Proposition 3.3 Any solution to Pell's equation must be a convergent of $\sqrt N$.
Proof: $(x - y \sqrt N )(x + y \sqrt N) = 1$. WLOG, we can assume $x$ and $y$ are both positive.
This gives $x-y\sqrt N=\frac{1}{x+y\sqrt N} < \frac{1}{2y\sqrt N}<\frac{1}{2y}$, so $\left |\frac{x}{y} - \sqrt N\right | < \frac{1}{2y^2}$. $\square$
This gives $x-y\sqrt N=\frac{1}{x+y\sqrt N} < \frac{1}{2y\sqrt N}<\frac{1}{2y}$, so $\left |\frac{x}{y} - \sqrt N\right | < \frac{1}{2y^2}$. $\square$
By considering the period of the continued fraction of $\sqrt N$, you can pick out the convergents that give solutions. Dirichlet's Unit Theorem merits a quick shout-out at this point - by pushing this line of reasoning further, you can show that the solutions to Pell's equation (corresponding to non-trivial units in $\mathbb{Q}(\displaystyle \sqrt N)$) form a (cyclic!) group, which is mind-blowingly cool.
A second application of continued fractions also exploits the nice properties of square roots - prime factorisation. This application is sort of technical, so I won't go into it right now, although I am planning a future post dedicated to prime factorisation algorithms.
There is a generalisation of continued fractions called (rather obscurely) "generalised continued fractions". I unfortunately do not have much to say about these at this point in time, other than the $\tan x$ example given in lectures was one of them.
This post has turned out to be massively long, as it was far too ambitious in scope. There are still a few details that I want to investigate in full depth at some point, but it's probably a better idea to do so in another post. I hope that anybody reading enjoyed it, and maybe learned something new.
Footnote: a significant number of these proofs are largely due to my Number Theory lecturer, Dr. Vicky Neale. A couple of them are due to my Topics in Analysis lecturer, Dr. Kovalev.
Sunday, 16 March 2014
Linear Analysis: Baire Category Theorem
The Baire Category Theorem is this year's big surprise for analysts (or it would have been, if Dr. Garling hadn't been so enthusiastic about it in Analysis II). Spanning the rift between topology and analysis like a mathematical bifrost, it allows us to link local properties such as openness to global properties such as denseness.
Proof: Take a sequence of nested open and closed balls, alternatingly. The centres of the closed balls give a Cauchy subsequence, if you shrink the balls fast enough, so there is a limit in the intersection by completeness. Equivalently, the intersection of a sequence of nested compact sets is non-empty in a complete metric space. $\square$
Proof: (using 1.1) Suppose $X=\bigcup^\infty F_n$, where the $F_n$ are closed. Set $U_n=X\backslash F_n$, which is open. Then $\bigcap^\infty U_n = \emptyset$, so one of the $U_n$ is not dense, from Theorem 1.1, which implies that one of the $F_n$ contains an open ball. $\square$
Proof of 1.1 assuming 1.2: This is fairly easy, using the observation that the complement of a nowhere dense set is a dense set, and vice-versa. In 1.1 we do not assume that $X$ is empty, so observe that if $X$ does happen to be empty, the intersection of any sequence of sets is dense, and so we are done. Suppose $U_n$ is a sequence of dense, open sets. Then $F_n=X\backslash U_n$ is a sequence of nowhere dense, closed sets. $\bigcap U_n = \bigcap (X\backslash F_n)= X\backslash \bigcup F_n \neq \emptyset$, where inequality follows from 1.2. We have currently only found one point in the intersection of the $U_n$, but this is another one of those cases where we are actually already done with no extra effort. Simply consider the subspace of $X$ given by the restriction of $X$ to any open ball to force the point we found to be where we want it. Thus, the intersection of the $U_n$ is in fact still dense. $\square$
Note that if you have any sequence of sets $F_n$ such that $X=\bigcup^\infty F_n$, you can apply BCT to their closures to conclude that they can't all be nowhere dense, strengthening the above statement slightly.
Here is some interesting mathematics that we didn't cover in lectures, but which is easily accessible using the notions we have developped. Baire introduced a classification of functions on the real line as a way of measuring how discontinuous they are.
The Baire class $n$ is a vector space[citation needed]. Several of the results that we have encountered (and a couple of extra-curricular, but relevant ones) can be rephrased rather pleasingly in terms of Baire classes, and $G_\delta$ language.
Culminating in a result which I promised someone on stackexchange I would get around to proving:
Question: what's an example of a Baire function that is not in any Baire class? Note that some sources extend to the definition of Baire classes to include a countable ordinal in the index. Perhaps the indicator function of a non-measurable set might do the trick?
[I am planning to come back to this post to include proofs of these results, and perhaps add some extra results. Example sheet 2 was a rough time for most of us, but it's incredibly rich - I'm gonna mine it for theorems harder than any Minecrafter ever mined for diamonds.]
Dense. A set $A \subset X$ is dense in $X$ if $\overline{A}=X$. Equivalently, $A$ is dense in $X$ if $A \cap N \neq \emptyset$ for any non-empty open set $N$ in $X$.
Nowhere dense. A set $A \subset X$ is nowhere dense in $X$ if $\text{int}(\overline{A})=\emptyset$.
Meagre. A meagre set is a countable union of nowhere dense sets.
1st category. Meagre.
2nd category. Not meagre.
Residual set. The complement of a meagre set.
Nowhere dense. A set $A \subset X$ is nowhere dense in $X$ if $\text{int}(\overline{A})=\emptyset$.
Meagre. A meagre set is a countable union of nowhere dense sets.
1st category. Meagre.
2nd category. Not meagre.
Residual set. The complement of a meagre set.
Theorem 1.1 (Baire Category Theorem I)
In a complete metric space, the intersection of countably many dense, open subsets is still dense.
In a complete metric space, the intersection of countably many dense, open subsets is still dense.
Proof: Take a sequence of nested open and closed balls, alternatingly. The centres of the closed balls give a Cauchy subsequence, if you shrink the balls fast enough, so there is a limit in the intersection by completeness. Equivalently, the intersection of a sequence of nested compact sets is non-empty in a complete metric space. $\square$
Theorem 1.2 (Baire Category Theorem II)
In a non-empty complete metric space $X$, the union of countably many closed, nowhere dense sets does not cover the whole space. Equivalently, if $X$ is the union of countably many closed sets, then one of those closed sets contains an open ball.
In a non-empty complete metric space $X$, the union of countably many closed, nowhere dense sets does not cover the whole space. Equivalently, if $X$ is the union of countably many closed sets, then one of those closed sets contains an open ball.
Proof: (using 1.1) Suppose $X=\bigcup^\infty F_n$, where the $F_n$ are closed. Set $U_n=X\backslash F_n$, which is open. Then $\bigcap^\infty U_n = \emptyset$, so one of the $U_n$ is not dense, from Theorem 1.1, which implies that one of the $F_n$ contains an open ball. $\square$
Proof of 1.1 assuming 1.2: This is fairly easy, using the observation that the complement of a nowhere dense set is a dense set, and vice-versa. In 1.1 we do not assume that $X$ is empty, so observe that if $X$ does happen to be empty, the intersection of any sequence of sets is dense, and so we are done. Suppose $U_n$ is a sequence of dense, open sets. Then $F_n=X\backslash U_n$ is a sequence of nowhere dense, closed sets. $\bigcap U_n = \bigcap (X\backslash F_n)= X\backslash \bigcup F_n \neq \emptyset$, where inequality follows from 1.2. We have currently only found one point in the intersection of the $U_n$, but this is another one of those cases where we are actually already done with no extra effort. Simply consider the subspace of $X$ given by the restriction of $X$ to any open ball to force the point we found to be where we want it. Thus, the intersection of the $U_n$ is in fact still dense. $\square$
Note that if you have any sequence of sets $F_n$ such that $X=\bigcup^\infty F_n$, you can apply BCT to their closures to conclude that they can't all be nowhere dense, strengthening the above statement slightly.
Remark 1.3.
The Baire Category Theorem is equivalent to the Axiom of Dependent Choice.
Applications of the Baire Category Theorem
| Result | Space | How? |
|---|---|---|
| Every complete metric space with no isolated points is uncountable. | Any complete space | Singleton sets are nowhere dense |
| There exist continuous nowhere differentiable functions. | $C[0,1]$, $\|.\|_\infty$ | The set of functions differentiable at some point is meagre. $Y_n = \{f \mid \exists x \in [0,1], \left|\frac{f(y)-f(x)}{y-x}\right| \leq n$, $\forall y \in [0,1]$, $y \neq x\}$ |
| Principle of uniform boundedness | Any Banach space. | $F_n=\{ x \in X \mid \|Tx\| \leq n, \forall T \in \tau\}$ |
| An infinite-dimensional Banach space has uncountable dimension | Any i.d. Banach space | $F_n=\text{span}\{e_1,\ldots,e_n\}$ |
| Open Mapping Theorem | $X$, $Y$ Banach spaces. $T$ surjective, continuous, linear. | $Y=\bigcup^\infty T(nB_x)$ |
| $f(nx) \to 0$ for each $x>0$, then $f(x) \to 0$ | $\mathbb{R}$ | $F_N=\{x \mid f(nx)\leq \varepsilon$, $\forall n \geq N\}$ |
Here is some interesting mathematics that we didn't cover in lectures, but which is easily accessible using the notions we have developped. Baire introduced a classification of functions on the real line as a way of measuring how discontinuous they are.
Define the set of Baire class zero functions to be the set of continuous functions. Define the set of Baire class $n$ functions to be the set of functions that are the pointwise limit of a sequence of Baire class $n-1$ functions.
The Baire class $n$ is a vector space[citation needed]. Several of the results that we have encountered (and a couple of extra-curricular, but relevant ones) can be rephrased rather pleasingly in terms of Baire classes, and $G_\delta$ language.
Theorem 1.4 The set of points of discontinuity of a Baire class one function is meagre. (See Ex2Q4+12.)
Theorem 1.5 The set of points of continuity of any function is a $G_\delta$ set. (See Ex2Q11.)
Theorem 1.6 The derivative of a differentiable function is Baire class one.
Culminating in a result which I promised someone on stackexchange I would get around to proving:
Theorem 1.7 The graph of a derivative is connected. (More generally, so is the graph of any function that is simultaneously Baire class one, and Darboux.)
Question: what's an example of a Baire function that is not in any Baire class? Note that some sources extend to the definition of Baire classes to include a countable ordinal in the index. Perhaps the indicator function of a non-measurable set might do the trick?
[I am planning to come back to this post to include proofs of these results, and perhaps add some extra results. Example sheet 2 was a rough time for most of us, but it's incredibly rich - I'm gonna mine it for theorems harder than any Minecrafter ever mined for diamonds.]
Saturday, 15 March 2014
Number Theory - Deriving Quadratic Reciprocity
There are allegedly dozens of proofs of quadratic reciprocity. Amazingly, not a single one of them is nice. (The undergraduate's definition of nice is something that can be easily remembered/regurgitated without thinking. All of the proofs of quadratic reciprocity that I have read involve pretty mind-bending arguments.)
This section involves extremely fiddly, annoying (or, put another way, marvellously creative, beautiful) mathematics. We need to be ready to get ours hands dirty, constructing bijections/partitions/relations between residue classes based on obscure/unwieldy properties. Good practice for tripos questions, I guess.
Proof: Take a primitive element, $g$. The quadratic residues are exactly the even powers of $g$.
Proof 2: $(-a)^2=a^2 \mod p$, so there are at most $\frac{p-1}{2}$ quadratic residues. $x^2 \equiv y^2 \mod p$ implies that $x \equiv \pm y \mod p$ (integral domain), so there are at least $\frac{p-1}{2}$ quadratic residues. $\square$
Proof: We will combine both proofs of the above lemma. We can assume $a$ coprime to $p$, as otherwise the claim is obvious (both sides are $0$).
First, note that $a^{p-1}\equiv 1 \mod p$ by Fermat's little theorem. Since we are working in an integral domain, $a^{\frac{p-1}{2}} \equiv \pm 1 \mod p$.
Let $g$ be a primitive element $\mod p$. Then $a=g^i$ for some $i$. If $i=2j$, then $a^{\frac{p-1}{2}}\equiv g^{(p-1)j} \equiv 1 \mod p$. Similarly, if $i$ is odd, then $a^{\frac{p-1}{2}} \equiv -1 \mod p$. Thus we have established that:
$$a^{\frac{p-1}{2}} = \left\{\begin{array}{ll} +1 & \text{if } a \text{ is an even power of } g \\ -1 & \text{if } a \text{ is an odd power of } g \end{array}\right.$$
From proof 1 above, this corresponds exactly to the value of the Legendre symbol $\left(\frac{a}{p}\right)$. $\square$
Proof: Observe that $\langle a \rangle, \langle 2a \rangle, \ldots, \langle \frac{p-1}{2}a\rangle$ are $\pm 1, \pm 2, \ldots, \pm \frac{p-1}{2}$ in some order, for some (fixed) choices of sign.
Hence, $(\frac{p-1}{2})!a^{\frac{p-1}{2}} \equiv \langle a \rangle \langle 2a \rangle \dots \langle (\frac{p-1}{2})a \rangle \equiv (-1)^\gamma (\frac{p-1}{2})! \mod p$.
By cancelling, $a^{\frac{p-1}{2}} \equiv (-1)^\gamma \mod p$. By Euler's criterion, $\left(\frac{a}{p}\right) \equiv (-1)^\gamma \mod p$. Since $(-1)^\gamma$ and $\left(\frac{a}{p}\right)$ are in $\{-1,1\}$, congruence implies equality. $\square$
Proof: To prove quadratic reciprocity, we use Gauss's lemma to rephrase the above assertion as the geometric problem of counting lattice points (points with integer coefficients in the plane) within specific regions of interest.
By the lemma, $\left(\frac{q}{p}\right)=(-1)^\gamma$, where $\gamma$ is as defined above.
We need to count how many of $\langle q \rangle, \langle 2q \rangle, \ldots, \langle \frac{p-1}{2} q \rangle$ are negative. (Note: we are working mod $p$.)
Observe that setting $\langle kq \rangle = kq - lp$ determines $l$ uniquely.
Thus, $\gamma$ corresponds to the number of lattice points $(k,l)$ within the region $-\frac{p}{2} < kq - lp < 0$. [more justification required]
Analagously, writing $\left(\frac{p}{q}\right)=(-1)^\beta$, Gauss's lemma says that $\beta$ corresponds to the number of lattice points $(k,l)$ within the region $-\frac{q}{2}< lp-kq < 0$.
Drawing the three (parallel) lines $kq-lp=-\frac{p}{2}$, $kq-lp=0$, and $kq-lp=\frac{q}{2}$ splits up the rectangle $0<k<p/2$, $0<l<q/2$ into four regions. From top left to bottom right, let's call them $A$ (a triangle), $B$ and $C$ (rhombuses), and $D$ (a triangle).
The total number of lattice points in the rectangle is $\frac{p-1}{2}\frac{q-1}{2}$ (recall that we are using strict inequality, so excluding those that fall on the axes). To prove quadratic reciprocity, we need the number of lattice points in $B$ and $C$ combined to have the same parity as $\frac{p-1}{2}\frac{q-1}{2}$.
We need two observations to see that this is true.
This section involves extremely fiddly, annoying (or, put another way, marvellously creative, beautiful) mathematics. We need to be ready to get ours hands dirty, constructing bijections/partitions/relations between residue classes based on obscure/unwieldy properties. Good practice for tripos questions, I guess.
Lemma 1.1 There are exactly $\frac{p-1}{2}$ quadratic residues $\mod p$.
Proof: Take a primitive element, $g$. The quadratic residues are exactly the even powers of $g$.
Proof 2: $(-a)^2=a^2 \mod p$, so there are at most $\frac{p-1}{2}$ quadratic residues. $x^2 \equiv y^2 \mod p$ implies that $x \equiv \pm y \mod p$ (integral domain), so there are at least $\frac{p-1}{2}$ quadratic residues. $\square$
Theorem 1.2 (Euler's criterion) $a^{\frac{p-1}{2}} \equiv \left(\frac{a}{p}\right) \mod p$.
Proof: We will combine both proofs of the above lemma. We can assume $a$ coprime to $p$, as otherwise the claim is obvious (both sides are $0$).
First, note that $a^{p-1}\equiv 1 \mod p$ by Fermat's little theorem. Since we are working in an integral domain, $a^{\frac{p-1}{2}} \equiv \pm 1 \mod p$.
Let $g$ be a primitive element $\mod p$. Then $a=g^i$ for some $i$. If $i=2j$, then $a^{\frac{p-1}{2}}\equiv g^{(p-1)j} \equiv 1 \mod p$. Similarly, if $i$ is odd, then $a^{\frac{p-1}{2}} \equiv -1 \mod p$. Thus we have established that:
$$a^{\frac{p-1}{2}} = \left\{\begin{array}{ll} +1 & \text{if } a \text{ is an even power of } g \\ -1 & \text{if } a \text{ is an odd power of } g \end{array}\right.$$
From proof 1 above, this corresponds exactly to the value of the Legendre symbol $\left(\frac{a}{p}\right)$. $\square$
Proposition 1.3 (Gauss's lemma)
We introduce least absolute value notation for a residue class mod $p$: write $\langle a \rangle$ for the unique integer congruent to $a \mod p$ lying in $[-p/2,p/2]$.
If $p$ is an odd prime, and $a$ is coprime to $p$, then $\left(\frac{a}{p}\right) = (-1)^\gamma$, where $\gamma = \#\{k \in \{1,2,\ldots,\frac{p-1}{2}\} \mid \langle ka \rangle < 0 \}$.
We introduce least absolute value notation for a residue class mod $p$: write $\langle a \rangle$ for the unique integer congruent to $a \mod p$ lying in $[-p/2,p/2]$.
If $p$ is an odd prime, and $a$ is coprime to $p$, then $\left(\frac{a}{p}\right) = (-1)^\gamma$, where $\gamma = \#\{k \in \{1,2,\ldots,\frac{p-1}{2}\} \mid \langle ka \rangle < 0 \}$.
Proof: Observe that $\langle a \rangle, \langle 2a \rangle, \ldots, \langle \frac{p-1}{2}a\rangle$ are $\pm 1, \pm 2, \ldots, \pm \frac{p-1}{2}$ in some order, for some (fixed) choices of sign.
Hence, $(\frac{p-1}{2})!a^{\frac{p-1}{2}} \equiv \langle a \rangle \langle 2a \rangle \dots \langle (\frac{p-1}{2})a \rangle \equiv (-1)^\gamma (\frac{p-1}{2})! \mod p$.
By cancelling, $a^{\frac{p-1}{2}} \equiv (-1)^\gamma \mod p$. By Euler's criterion, $\left(\frac{a}{p}\right) \equiv (-1)^\gamma \mod p$. Since $(-1)^\gamma$ and $\left(\frac{a}{p}\right)$ are in $\{-1,1\}$, congruence implies equality. $\square$
Theorem 1.4 (Quadratic reciprocity)
Let $p$ and $q$ be odd primes. Then $\left(\frac{q}{p}\right) = (-1)^{\frac{p-1}{2}\frac{q-1}{2}}\left(\frac{p}{q}\right)$.
If we assume $p$ and $q$ to be distinct, we can reformulate as $\left(\frac{q}{p}\right)\left(\frac{p}{q}\right) = (-1)^{\frac{p-1}{2}\frac{q-1}{2}}$.
Let $p$ and $q$ be odd primes. Then $\left(\frac{q}{p}\right) = (-1)^{\frac{p-1}{2}\frac{q-1}{2}}\left(\frac{p}{q}\right)$.
If we assume $p$ and $q$ to be distinct, we can reformulate as $\left(\frac{q}{p}\right)\left(\frac{p}{q}\right) = (-1)^{\frac{p-1}{2}\frac{q-1}{2}}$.
Proof: To prove quadratic reciprocity, we use Gauss's lemma to rephrase the above assertion as the geometric problem of counting lattice points (points with integer coefficients in the plane) within specific regions of interest.
By the lemma, $\left(\frac{q}{p}\right)=(-1)^\gamma$, where $\gamma$ is as defined above.
We need to count how many of $\langle q \rangle, \langle 2q \rangle, \ldots, \langle \frac{p-1}{2} q \rangle$ are negative. (Note: we are working mod $p$.)
Observe that setting $\langle kq \rangle = kq - lp$ determines $l$ uniquely.
Thus, $\gamma$ corresponds to the number of lattice points $(k,l)$ within the region $-\frac{p}{2} < kq - lp < 0$. [more justification required]
Analagously, writing $\left(\frac{p}{q}\right)=(-1)^\beta$, Gauss's lemma says that $\beta$ corresponds to the number of lattice points $(k,l)$ within the region $-\frac{q}{2}< lp-kq < 0$.
Drawing the three (parallel) lines $kq-lp=-\frac{p}{2}$, $kq-lp=0$, and $kq-lp=\frac{q}{2}$ splits up the rectangle $0<k<p/2$, $0<l<q/2$ into four regions. From top left to bottom right, let's call them $A$ (a triangle), $B$ and $C$ (rhombuses), and $D$ (a triangle).
The total number of lattice points in the rectangle is $\frac{p-1}{2}\frac{q-1}{2}$ (recall that we are using strict inequality, so excluding those that fall on the axes). To prove quadratic reciprocity, we need the number of lattice points in $B$ and $C$ combined to have the same parity as $\frac{p-1}{2}\frac{q-1}{2}$.
We need two observations to see that this is true.
- There is a bijection between $A$ and $D$.
- None of the lattice points are on any of the three lines that we drew. The lecturer totally failed to discuss this point, but it is crucial - given that we are considering strict inequality, if a lattice point was on one of the lines it wouldn't be counted in any of the regions (and if we were considering non-strict inequality, it would be counted twice). Luckily, this can't happen as $p$ and $q$ are prime.
Combining these two observations means that $|B|+|C|+2|A| = \frac{p-1}{2}\frac{q-1}{2}$, and so $|B| + |C|$ and $\frac{p-1}{2}\frac{q-1}{2}$ have the same parity. From Gauss's lemma, above, we showed that $\left(\frac{q}{p}\right)\left(\frac{p}{q}\right) = (-1)^\gamma(-1)^\beta=(-1)^{|B|+|C|}$, and the statement of quadratic reciprocity is $\left(\frac{q}{p}\right)\left(\frac{p}{q}\right) = (-1)^{\frac{p-1}{2}\frac{q-1}{2}}$, so we are done.
Let's prove 2 first. Suppose a point $(k,l)$ is on the line $kq-lp=0$, and that $k$ is an integer. Then $l=k\frac{q}{p}$, so $l$ isn't an integer. Similarly, if $k$ is an integer, then $l=k\frac{q}{p}+\frac{1}{2}$ isn't, and neither is $l=\frac{q}{p}(k-\frac{1}{2})$. Phew.
For 1, the required bijection is given by $(k,l) \leftrightarrow \left(\frac{p+1}{2}-k, \frac{q+1}{2}-l\right)$ (the same formula works both ways, from $A$ to $D$ and from $D$ to $A$). Visually, you pick up the bottom right triangle, rotate it 180 degrees, and slap it back onto the top right triangle. It doesn't fit together exactly, but instead overlaps egregiously, so it's really quite remarkable that this works. The lecturer left it as an exercice to prove that this bijection indeed does the job (I'm getting the impression that this proof is unlikely to come up in the exam).
The map is clearly injective from the above observation that the formula is self-inverse, i.e. applying it twice recovers the same point. So we only need to check that this map is well-defined, i.e. maps $C$ into $D$, and is surjective. Well-definedness is easy to obtain from definition-chasing. There is no extra work in obtaining surjectivity - it follows from well-definedness in the other direction. So we are done. $\square$
For 1, the required bijection is given by $(k,l) \leftrightarrow \left(\frac{p+1}{2}-k, \frac{q+1}{2}-l\right)$ (the same formula works both ways, from $A$ to $D$ and from $D$ to $A$). Visually, you pick up the bottom right triangle, rotate it 180 degrees, and slap it back onto the top right triangle. It doesn't fit together exactly, but instead overlaps egregiously, so it's really quite remarkable that this works. The lecturer left it as an exercice to prove that this bijection indeed does the job (I'm getting the impression that this proof is unlikely to come up in the exam).
The map is clearly injective from the above observation that the formula is self-inverse, i.e. applying it twice recovers the same point. So we only need to check that this map is well-defined, i.e. maps $C$ into $D$, and is surjective. Well-definedness is easy to obtain from definition-chasing. There is no extra work in obtaining surjectivity - it follows from well-definedness in the other direction. So we are done. $\square$
Number Theory - The structure of multiplicative groups of integers
This post aims to establish the basics about multiplicative groups as clearly and as efficiently as possible. I will include the proofs given in lectures to start off with, but I plan to trawl around for better alternatives.
0. Elementary stuff you should know how to prove by now
1 Note to self: it feels like there is something more to be said here. Link to lattices?
0. Elementary stuff you should know how to prove by now
- Division algorithm for integers/polynomials in an integral domain
- Bezout
- Existence and uniqueness of prime factorisation
1. For $p$ prime, $\left(\mathbb{Z}/p\mathbb{Z}\right)^\times$ is cyclic
In other words, there always exists a primitive element $\mod p$ for $p$ prime. This theorem is very well-known, and feels trivial. It's not - there is a lot of groundwork that simply can't be avoided.
Intermediate results:
1.1 Lagrange's theorem for polynomials
In an integral domain, a polynomial of degree $d$ can have at most $d$ roots.
Proof:
We induct on the degree of the polynomial.
For $n=1$, write $p(x)=ax+b$, $a \neq 0$.
Suppose there are two distinct solutions, $x$ and $y$. Then, by subtracting, $a(x-y)=0$. In an integral domain, this implies $x=y$.
For the inductive step, the division algorithm for polynomials (which is valid in an integral domain) implies that for any root $x_0$ of a polynomial $p$, $p$ can be factored as $(x-x_0)g(x)$. In an integral domain, the degree of a product of polynomials is the sum of the degrees of the factors. Thus, $p$ has at most one more root than $g$, and so at most $n$ roots in total, by the induction hypothesis. $\square$
1.2 For $p$ prime, $F = \mathbb{Z}/p\mathbb{Z}$ is a field
Proof:
Pick any non-zero element $a$. We need to find an inverse for $a$.
Define a map $\phi_a : F \to F$ by $\phi_a(z)=az$. This is an injection, as $F$ is an integral domain (immediate from the definition of a prime number). An injection from a finite set to itself must necessarily be a surjection. Thus, $ab=1$ for some $b \in F$, proving that $a$ has a multiplicative inverse. $\square$
1.3 The Euler totient function $\phi$ is multiplicative
Note: $\phi$ is not totally multiplicative. E.g. $\phi(2)=1$, $\phi(4)=2$.
We define $\phi(n)$ as the number of positive integers less than $n$ that are coprime to $n$, and observe that Bezout implies that $\phi(n)= \left| (\mathbb{Z}/n\mathbb{Z})^\times \right|$.
Proof:
The Chinese Remainder Theorem gives a bijection (more precisely, an isomorphism) between $\left(\mathbb{Z}/m_1m_2\mathbb{Z}\right)^\times$ and $\left(\mathbb{Z}/m_1\mathbb{Z}\right)^\times\times\left(\mathbb{Z}/m_2\mathbb{Z}\right)^\times$ whenever $m_1$ and $m_2$ are coprime, giving $\phi(m_1m_2)=\phi(m_1)\phi(m_2)$. $\square$
1.4 The Eulier totient function has the property: $\displaystyle \sum_{d \mid n} \phi(d) = n$.
Proof:
We establish the fact that for any multiplicative function $\varphi$, $F(n) = \displaystyle \sum_{d \mid n} \varphi(d)$ is also multiplicative.1
Let $m$ and $n$ be coprime. Then:
$$F(mn)=\displaystyle \sum_{d \mid m_1} \varphi(d) = \sum_{d_1 \mid m, d_2 \mid n} \varphi(d_1d_2)$$$$ = \sum_{d_1 \mid m, d_2 \mid n} \varphi(d_1)\varphi(d_2) = \left(\sum_{d_1 \mid m} \varphi(d_1)\right)\left(\sum_{d_2 \mid n} \varphi(d_2)\right)$$$$=F(m)F(n)$$
Observe that $\phi(p^k)=p^{k-1}(p-1)$, so $F_\phi(p^k)=1 + (p-1) + \dots + (p^k-p^{k-1}) = p^k$. Thus, $F_\phi(n)=F_\phi(p_1^{n_1}\dots p_k^{n_k})=p_1^{n_1}\dots p_k^{n_k}=n$. $\square$
Proof of 1.
For each divisor $d$ of $p-1$, we show that if there is an element of order $d$, there must in fact be (exactly) $\phi(d)$ elements of order $d$. Thus, if $S_d$ is the set of elements of order $d$, then $|S_d|=\phi(d)$, or $|S_d|=0$. Since $\displaystyle \sum_{d \mid p-1} (\phi(d) - |S_d|) = p-1 - (p-1) = 0$, it follows that $|S_d|=\phi(d)$ for each $d$ dividing $p-1$ (if any of the $|S_d|$ are empty, the above formula can't hold), and so in particular $S_{p-1}$ is non-empty.
Let $a$ be an element of order $d$. By Lagrange's theorem $x^{d} \equiv 1 \mod p$ has at most $d$ solutions. Any element of order $d$ is a solution to this equation. But we can list $d$ distinct solutions: $1,a,a^2,\ldots,a^{d-1}$. Observe that $a^k$ has order $d$ exactly when $(d,k)=1$. Thus, there are exactly $\phi(d)$ elements of order $d$. $\square$
We call the elements of order $p-1$ the primitive roots $\mod p$. From the above, there are $\phi(p-1)$ of them.
2. For $p$ an odd prime, $\left(\mathbb{Z}/p^k\mathbb{Z})\right)^\times$ is cyclic for any $k$.
We prove this by exhibiting an element of order $p^{k-1}(p-1)$.
Let $g_1$ be a primitive element of $\left(\mathbb{Z}/p\mathbb{Z})\right)^\times$.
Compute $g_1^{p-1}-1 \mod p^2$. If it's zero, set $g=g_1+p$. If it's non-zero, set $g=g_1$.
Then $g$ generates $\left(\mathbb{Z}/p^k\mathbb{Z})\right)^\times$.
We have chosen $g$ such that $g^{p-1}=1+bp$, where $b$ is coprime to $p$.
Thus, $g^{p^{k-1}(p-1)}=(1+bp)^{p^{k-1}}=1+bp{p^{k-1} \choose 1}+ \dots \equiv 1 \mod p^{k}$. So the order of $g$ (mod $p^k$) divides $p^{k-1}(p-1)$, and doesn't divide $p-1$.
Noting that $g^{p^{k-2}(p-1)}=(1+bp)^{p^{k-2}}=1+bp{p^{k-2} \choose 1} + (bp)^2{p^{k-2} \choose 2} + \dots \not\equiv 1 \mod p^{k}$, we can conclude that $g$ has order exactly $p^{k-1}(p-1)$, and so $\left(\mathbb{Z}/p^k\mathbb{Z})\right)^\times$ is cyclic. $\square$
3. Reserved space for other relevant results/properties proved on example sheets
In other words, there always exists a primitive element $\mod p$ for $p$ prime. This theorem is very well-known, and feels trivial. It's not - there is a lot of groundwork that simply can't be avoided.
Intermediate results:
1.1 Lagrange's theorem for polynomials
In an integral domain, a polynomial of degree $d$ can have at most $d$ roots.
Proof:
We induct on the degree of the polynomial.
For $n=1$, write $p(x)=ax+b$, $a \neq 0$.
Suppose there are two distinct solutions, $x$ and $y$. Then, by subtracting, $a(x-y)=0$. In an integral domain, this implies $x=y$.
For the inductive step, the division algorithm for polynomials (which is valid in an integral domain) implies that for any root $x_0$ of a polynomial $p$, $p$ can be factored as $(x-x_0)g(x)$. In an integral domain, the degree of a product of polynomials is the sum of the degrees of the factors. Thus, $p$ has at most one more root than $g$, and so at most $n$ roots in total, by the induction hypothesis. $\square$
1.2 For $p$ prime, $F = \mathbb{Z}/p\mathbb{Z}$ is a field
Proof:
Pick any non-zero element $a$. We need to find an inverse for $a$.
Define a map $\phi_a : F \to F$ by $\phi_a(z)=az$. This is an injection, as $F$ is an integral domain (immediate from the definition of a prime number). An injection from a finite set to itself must necessarily be a surjection. Thus, $ab=1$ for some $b \in F$, proving that $a$ has a multiplicative inverse. $\square$
1.3 The Euler totient function $\phi$ is multiplicative
Note: $\phi$ is not totally multiplicative. E.g. $\phi(2)=1$, $\phi(4)=2$.
We define $\phi(n)$ as the number of positive integers less than $n$ that are coprime to $n$, and observe that Bezout implies that $\phi(n)= \left| (\mathbb{Z}/n\mathbb{Z})^\times \right|$.
Proof:
The Chinese Remainder Theorem gives a bijection (more precisely, an isomorphism) between $\left(\mathbb{Z}/m_1m_2\mathbb{Z}\right)^\times$ and $\left(\mathbb{Z}/m_1\mathbb{Z}\right)^\times\times\left(\mathbb{Z}/m_2\mathbb{Z}\right)^\times$ whenever $m_1$ and $m_2$ are coprime, giving $\phi(m_1m_2)=\phi(m_1)\phi(m_2)$. $\square$
1.4 The Eulier totient function has the property: $\displaystyle \sum_{d \mid n} \phi(d) = n$.
Proof:
We establish the fact that for any multiplicative function $\varphi$, $F(n) = \displaystyle \sum_{d \mid n} \varphi(d)$ is also multiplicative.1
Let $m$ and $n$ be coprime. Then:
$$F(mn)=\displaystyle \sum_{d \mid m_1} \varphi(d) = \sum_{d_1 \mid m, d_2 \mid n} \varphi(d_1d_2)$$$$ = \sum_{d_1 \mid m, d_2 \mid n} \varphi(d_1)\varphi(d_2) = \left(\sum_{d_1 \mid m} \varphi(d_1)\right)\left(\sum_{d_2 \mid n} \varphi(d_2)\right)$$$$=F(m)F(n)$$
Observe that $\phi(p^k)=p^{k-1}(p-1)$, so $F_\phi(p^k)=1 + (p-1) + \dots + (p^k-p^{k-1}) = p^k$. Thus, $F_\phi(n)=F_\phi(p_1^{n_1}\dots p_k^{n_k})=p_1^{n_1}\dots p_k^{n_k}=n$. $\square$
Proof of 1.
For each divisor $d$ of $p-1$, we show that if there is an element of order $d$, there must in fact be (exactly) $\phi(d)$ elements of order $d$. Thus, if $S_d$ is the set of elements of order $d$, then $|S_d|=\phi(d)$, or $|S_d|=0$. Since $\displaystyle \sum_{d \mid p-1} (\phi(d) - |S_d|) = p-1 - (p-1) = 0$, it follows that $|S_d|=\phi(d)$ for each $d$ dividing $p-1$ (if any of the $|S_d|$ are empty, the above formula can't hold), and so in particular $S_{p-1}$ is non-empty.
Let $a$ be an element of order $d$. By Lagrange's theorem $x^{d} \equiv 1 \mod p$ has at most $d$ solutions. Any element of order $d$ is a solution to this equation. But we can list $d$ distinct solutions: $1,a,a^2,\ldots,a^{d-1}$. Observe that $a^k$ has order $d$ exactly when $(d,k)=1$. Thus, there are exactly $\phi(d)$ elements of order $d$. $\square$
We call the elements of order $p-1$ the primitive roots $\mod p$. From the above, there are $\phi(p-1)$ of them.
2. For $p$ an odd prime, $\left(\mathbb{Z}/p^k\mathbb{Z})\right)^\times$ is cyclic for any $k$.
We prove this by exhibiting an element of order $p^{k-1}(p-1)$.
Let $g_1$ be a primitive element of $\left(\mathbb{Z}/p\mathbb{Z})\right)^\times$.
Compute $g_1^{p-1}-1 \mod p^2$. If it's zero, set $g=g_1+p$. If it's non-zero, set $g=g_1$.
Then $g$ generates $\left(\mathbb{Z}/p^k\mathbb{Z})\right)^\times$.
We have chosen $g$ such that $g^{p-1}=1+bp$, where $b$ is coprime to $p$.
Thus, $g^{p^{k-1}(p-1)}=(1+bp)^{p^{k-1}}=1+bp{p^{k-1} \choose 1}+ \dots \equiv 1 \mod p^{k}$. So the order of $g$ (mod $p^k$) divides $p^{k-1}(p-1)$, and doesn't divide $p-1$.
Noting that $g^{p^{k-2}(p-1)}=(1+bp)^{p^{k-2}}=1+bp{p^{k-2} \choose 1} + (bp)^2{p^{k-2} \choose 2} + \dots \not\equiv 1 \mod p^{k}$, we can conclude that $g$ has order exactly $p^{k-1}(p-1)$, and so $\left(\mathbb{Z}/p^k\mathbb{Z})\right)^\times$ is cyclic. $\square$
3. Reserved space for other relevant results/properties proved on example sheets
1 Note to self: it feels like there is something more to be said here. Link to lattices?
Subscribe to:
Comments (Atom)

