This computer-assisted proof of the Four-Colour Theorem was catalytic (maybe even cataclysmic) in the maths world, challenging the sanctity of home-baked proofs traditionally written in sweat and blood. Historically, the meta-mathematical discussion resulting from this event has often been misrepresented - mathematicians did not object to the computer-assisted approach out of elitism or Luddism, but were genuinely uneasy about how they could be sure that the proposed solution actually constituted an acceptable proof. As it turns out, these misgivings were entirely justified - a team of researchers attempting to verify the original proof of the four-colour theorem were unable to decipher and reproduce the method from the 1976 paper, and were forced to come up with their own solution.
The proof of the FCT has been simplified and improved over the years, but still requires significant computer assistance, so it's understandable that it didn't feature in our course. We did however prove the weaker 5-colour theorem, and derived a very attractive equivalent formulation of the FCT. We also introduced and discussed a couple of interesting objects that were designed in an attempt to prove the FCT. One example is the chromatic polynomial $P_G(x)$, equal to the number of colourings of a graph $G$ in $x$ colours (it's a polynomial for combinatorial reasons). However, in an attempt to limit the scope of my post, I will leave the chromatic polynomial for another day.
The chromatic number of a graph $G$, written $\chi(G)$, is the minimum number of colours required to colour the vertices of $G$ such that no two adjacent vertices have the same colour.
Observe that a $k$-colouring of a graph immediately gives a $k$-partition of the vertices of $G$ with no edges within each partition, so colourings are actually highly valuable in practice.
In general, we are interested in the problem of finding an upper bound for $\chi(G)$. The greedy algorithm gives a first stab at this, but usually performs pretty awfully.
Note that the chromatic number is related to vertex-colourings, whereas the FCT concerns face-colourings. The following construction relates the two problems for the class of planar graphs.
The dual graph $G^\prime$ of $G$ is the graph obtained by placing a vertex inside each face of $G$, and linking two vertexes together (in $G^\prime$) whenever the corresponding faces are continguous (in $G$). Visually, we draw one dual edge through each existing edge.
Above is an example of a self-dual graph on 5 vertices. Note that in general, the dual graph of a planar graph may fail to be simple (i.e. there could be could be multiple edges between two vertices, if $G$ has two faces that share multiple edges, or if there is a bridge). One sufficient condition for the dual to be simple is for $G$ to be $3$-connected, which means that removing any two vertices (and their incident edges) would not suffice to disconnect the graph.
Clearly the dual is planar. You can also visually recognise quite easily that the double-dual is naturally isomorphic to the original graph.
Observation. A vertex-colouring of $G$ is equivalent to a face-colouring of the dual graph $G^\prime$.
Thus, proving that $\chi(G) \leq 4$ for every planar graph is equivalent to the usual statement of the FCT, which asserts that every bridgeless plane map can be face-coloured with four colours. (Quick terminological clarification - map indicates that we are referring to the faces of the graph. A plane graph (or map) is a given instance/embedding/realisation of a planar graph (or map), which is an abstract object. A planar graph can have several different plane graphs whose faces have different numbers of edges, although Euler's formula guarantees that the number of faces must remain constant.)
The following, weaker statement can be proven relatively easily from basic principles.
Theorem. (Five-Colour Theorem)
If $G$ is a planar graph, then $\chi(G)\leq 5$.
If $G$ is a planar graph, then $\chi(G)\leq 5$.
Proof: Suppose not. Let $G$ be a minimal counterexample.
Recall (from an earlier post) that for any planar graph, the minimum degree $\delta(G)$ satisfies $\delta(G) \leq 5$.
We first consider the case $\delta(G) \leq 4$. Let $v$ be a vertex of degree $\leq 4$. By minimality, we can colour $G-v$ with 5 colours. But $v$ has at most 4 neighbours in $G$, so we can certainly colour $v$ with one of the 5 colours, giving a 5-colouring of $G$.
So we may assume $\delta(G)=5$.
Pick a vertex of degree 5, with neighbours $v_1$, $v_2$, $v_3$, $v_4$, and $v_5$.
$K_5$ is non-planar, so is not a subgraph of $G$. Thus, we can pick $v_i$ and $v_j$ such that $v_iv_j$ is not an edge. We construct a new graph, $G^\prime$, by removing $v$, and identifying $v_i$ and $v_j$.
This graph is planar by construction, so can be 5-coloured by minimality.
But we can use this colouring to colour $G$. In $G$, colour both $v_i$ and $v_j$ the same colour as the identified vertex in $G^\prime$ (every other vertex apart from $v$ can keep its colour). But now the neighbours of $v$ use only 4 colours, so we can use the 5th colour to complete the 5-colouring of $G$. $\square$
Recall (from an earlier post) that for any planar graph, the minimum degree $\delta(G)$ satisfies $\delta(G) \leq 5$.
We first consider the case $\delta(G) \leq 4$. Let $v$ be a vertex of degree $\leq 4$. By minimality, we can colour $G-v$ with 5 colours. But $v$ has at most 4 neighbours in $G$, so we can certainly colour $v$ with one of the 5 colours, giving a 5-colouring of $G$.
So we may assume $\delta(G)=5$.
Pick a vertex of degree 5, with neighbours $v_1$, $v_2$, $v_3$, $v_4$, and $v_5$.
$K_5$ is non-planar, so is not a subgraph of $G$. Thus, we can pick $v_i$ and $v_j$ such that $v_iv_j$ is not an edge. We construct a new graph, $G^\prime$, by removing $v$, and identifying $v_i$ and $v_j$.
This graph is planar by construction, so can be 5-coloured by minimality.
But we can use this colouring to colour $G$. In $G$, colour both $v_i$ and $v_j$ the same colour as the identified vertex in $G^\prime$ (every other vertex apart from $v$ can keep its colour). But now the neighbours of $v$ use only 4 colours, so we can use the 5th colour to complete the 5-colouring of $G$. $\square$
Here is a visual example of the construction used in the above proof:
 |
 |
| $G$ | $G^\prime$ |
The Four-Colour Theorem improves upon the above result by showing that $\chi(G)\leq4$ for every planar graph $G$. It is a best possible result - the planar graph $K_4$ certainly requires four distinct colours. As remarked above, its proof is everything but elementary. However, there is an interesting reformulation of the problem that we will take a moment to consider.
We define $\chi^\prime(G)$, the edge-chromatic number, to be the minimum number of colours needed to colours the edges of $G$ such that no two adjacent edges are coloured the same.
A cubic graph is a 3-regular graph, meaning that every vertex has exactly three neighbours.
Observation. To prove the FLT (in it's face-colouring form), we may assume that $G$ is cubic.
At any vertex with degree more than three, we can consider instead the graph obtained by introducing a polygonal roundabout. A face-colouring of the latter induces a face-colouring of the former.
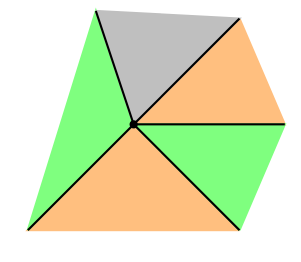 |

|
Theorem (Tait)
The FCT holds $\Leftrightarrow$ $\chi^\prime(G)=3$ for every cubic planar bridgeless graph $G$.
The FCT holds $\Leftrightarrow$ $\chi^\prime(G)=3$ for every cubic planar bridgeless graph $G$.
Proof: Let $G$ be a cubic bridgeless planar graph. We show that $G$ can be face 4-coloured $\Leftrightarrow$ $G$ can be edge 3-coloured.
Consider $\mathbb{Z}_2\times\mathbb{Z}_2$ as an additive group - containing four elements: 00, 01, 10, 11. These will be our four face-colours, and we will find a corresponding edge-colouring using only 01,10 and 11.
Given a face colouring, let each edge be coloured with the sum of the two bordering face colours. Since $G$ is bridgeless, no edge will be coloured 00. Also, no two adjacent edges will get the same colour, as $a+c \neq b+c$ if $a \neq b$ (recall that we are considering cubic graphs, so there are always exactly three edges incident to a given vertex).
Given an edge colouring, we need to find a face 4-colouring. We will do this by vertex-colouring the dual (observe that the dual of a cubic graph is a triangulation). Each edge of the dual crosses exactly one edge in the original graph. For each edge in the dual, record this initial colour (as a label).
Pick a vertex $v_0$ in the dual, and colour it 00. To obtain the final colour for any other vertex $v$, sum up the labels along any path between $v_0$ and $v$.
The sum of the labels around any triangle is 10+01+11=00, and so the sum of the labels around any cycle vanishes. This proves that the sum of the labels along a path between $v$ and $v_0$ is independent of the path, so the above colouring is well-defined. $\square$
Consider $\mathbb{Z}_2\times\mathbb{Z}_2$ as an additive group - containing four elements: 00, 01, 10, 11. These will be our four face-colours, and we will find a corresponding edge-colouring using only 01,10 and 11.
Given a face colouring, let each edge be coloured with the sum of the two bordering face colours. Since $G$ is bridgeless, no edge will be coloured 00. Also, no two adjacent edges will get the same colour, as $a+c \neq b+c$ if $a \neq b$ (recall that we are considering cubic graphs, so there are always exactly three edges incident to a given vertex).
Given an edge colouring, we need to find a face 4-colouring. We will do this by vertex-colouring the dual (observe that the dual of a cubic graph is a triangulation). Each edge of the dual crosses exactly one edge in the original graph. For each edge in the dual, record this initial colour (as a label).
Pick a vertex $v_0$ in the dual, and colour it 00. To obtain the final colour for any other vertex $v$, sum up the labels along any path between $v_0$ and $v$.
The sum of the labels around any triangle is 10+01+11=00, and so the sum of the labels around any cycle vanishes. This proves that the sum of the labels along a path between $v$ and $v_0$ is independent of the path, so the above colouring is well-defined. $\square$
In my humble opinion, that proof is pretty damn awesome. Don't you agree?
Credit for the wording of the proofs should go to Prof. Thomason.

No comments:
Post a Comment